CHAPTER 14
MOBILE ROBOTS
In this chapter we discuss the control of nonholonomic systems with a focus on the control of mobile robots. Mobile robots are becoming increasingly important in many applications, such as factory and warehouse automation, service and cleaning, household and medical assistance, military applications, agricultural and forestry applications, and search and rescue. Autonomous highway vehicles (cars and trucks) can also be considered mobile robots.
A distinguishing feature of mobile robots that impacts the control problem is the presence of nonholonomic constraints. Nonholonomic constraints arise in two primary ways.
- In rolling without slipping constraints. For example, the translation and rotation of a wheel are not independent if the wheel rolls without slipping. Examples include:
- A wheeled mobile robot, unicycle, automobile, or tractor/trailer
- Manipulation of rigid objects, for example, fingers in rolling contact with an object
- In systems where angular momentum is conserved. Examples include:
- Satellites and space robots
- Gymnastic, diving, and running robots
We will mainly focus in this chapter on the control of wheeled mobile robots, which are part of a particular class of systems known as driftless systems, which we define later. These systems are examples of underactuated systems that are not linearly controllable according to Definition 13.3 in Chapter 13.
We first discuss the notion of nonholonomic constraints and nonholonomic systems, which we introduced briefly in Chapter 6. Understanding the difference between holonomic and nonholomic constraints is fundamental to the understanding of every concept introduced in this chapter. We then discuss the problems of controllability and stabilizability for mobile robots and outline both open-loop and closed-loop control methods for the problems of set-point regulation and trajectory tracking. The main theoretical control results we will discuss are Chow’s theorem and Brockett’s theorem. Chow’s theorem gives necessary and sufficient conditions for a driftless system to be controllable. Brockett’s theorem gives a necessary condition for stabilization of such systems by smooth feedback control.
14.1 Nonholonomic Constraints
We introduced holonomic constraints in Chapter 6 when we derived the Euler–Lagrange equations of motion for rigid manipulators. We saw that interconnecting n rigid bodies, each of which independently has 6 degrees of freedom, with revolute or prismatic joints, introduces holonomic constraints that reduce the number of degrees of freedom from 6n to just n. Our treatment of force control in Chapter 10 dealt with unilateral constraints, which are imposed by contact between the robot and the environment. In this section we expand upon the notion of systems subject to constraints and discuss nonholonomic constraints.
Let (q1, …, qn) denote a coordinate representation of the configuration q in the configuration space  of a given system. We recall the following definition from Section (6.1.2).
of a given system. We recall the following definition from Section (6.1.2).
Definition 14.1. (Holonomic constraint).
An equality constraint of the form
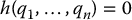
where h is a mapping from  is called a holonomic constraint. We assume that the function h is continuously differentiable and that the differential
is called a holonomic constraint. We assume that the function h is continuously differentiable and that the differential  is nonzero at each
is nonzero at each  .
.
As a result of this holonomic constraint, the configuration of the system, q = (q1, …, qn), is restricted to an n − 1 dimensional manifold in the configuration space defined by Equation (14.1).
Example 14.1.
A simple example of a system subject to a holonomic constraint is a mass m attached to the end of a rigid rod of length ℓ that is pinned to the origin and free to rotate in the plane. The (x, y) coordinates of the mass therefore satisfy the holonomic constraint
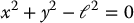
which constrains the motion of the mass to the circle of radius ℓ in  .
.

Figure 14.1 Mass m connected to a rigid rod.
We often have constraints that are expressed as functions of both the configurations and velocities as  , where the function
, where the function  is continuously differentiable in both arguments. We will limit our discussion to so-called Pfaffian constraints, as defined next
is continuously differentiable in both arguments. We will limit our discussion to so-called Pfaffian constraints, as defined next
Definition 14.2. (Pfaffian constraint).
Constraints of the form

where the row vector w(q) = (w1(q), …, wn(q)) is a covector in the cotangent space  , are called Pfaffian constraints.
, are called Pfaffian constraints.
Note that the constraint given by Equation (14.3) constrains the velocity vector  at each q but does not necessarily constrain the configuration q to a lower dimensional manifold. Stated another way, at each configuration q, Equation (14.3) specifies the allowable velocities.
at each q but does not necessarily constrain the configuration q to a lower dimensional manifold. Stated another way, at each configuration q, Equation (14.3) specifies the allowable velocities.
If the configuration q(t) is constrained by the holonomic constraint in Equation (14.1) for all time t ⩾ 0 it follows that
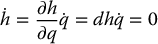
Thus we can say that a Pfaffian constraint  is holonomic if there exists a function
is holonomic if there exists a function  such that
such that
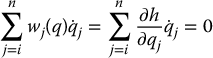
This, in turn, implies the existence of a function γ(q), called an integrating factor such that
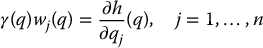
In this case, the constraint  is referred to as integrable. Note that if the constraint is integrable, it follows, since h is continuously differentiable, that
is referred to as integrable. Note that if the constraint is integrable, it follows, since h is continuously differentiable, that
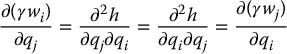
This leads to the following necessary and sufficient conditions for a Pfaffian constraint to be integrable.
Proposition 14.1
Equation (14.3) defines an integrable (holonomic) constraint, if and only if there exists a nonzero function γ(q) such that the components wi of w satisfy
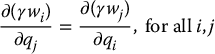
Example 14.2.
Consider the Pfaffian constraint on 
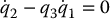
which is of the form  with w = ( − q3, 1, 0). A simple calculation, using Equation (14.6), shows that
with w = ( − q3, 1, 0). A simple calculation, using Equation (14.6), shows that
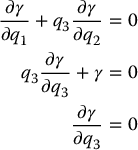
It is easy to see from the above that the only possible solution is γ = 0 (Problem 14–1). Therefore the constraint is nonholonomic.
Multiple Constraints
Suppose now that we have k ⩾ 2 Pfaffian constraints
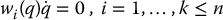
where each covector wi(q) is given by wi(q) = (wi1(q), …, win(q)).
Example 14.3.
We note that checking the holonomy of each constraint separately does not give us sufficient information about the constraints on the system configuration. Consider the two Pfaffian constraints
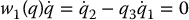
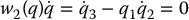
One can check that individually these constraints are nonholonomic. In fact, we showed the nonholonomy of the constraint given by Equation (14.9) in Example 14.2 above. Note, however, that the linear combination q1w1 + w2 satisfies

which can be integrated to  and
and  (Problem 14–2). Therefore, the constraints are holonomic. In fact, it will follow from Theorem 14.1 below that any set of n − 1 Pfaffian constraints in
(Problem 14–2). Therefore, the constraints are holonomic. In fact, it will follow from Theorem 14.1 below that any set of n − 1 Pfaffian constraints in  is holonomic.
is holonomic.
We can express a set of multiple Pfaffian constraints, as in Equation (14.8) as a matrix equation
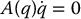
where A is the k × n matrix

Note that  means that the velocity
means that the velocity  lies in the null space of A(q) for each q. If the rank of A(q) is equal to k, implying that the constraints are independent, then there will be an m = n − k-dimensional null space of A. Let {g1(q), …, gm(q)} be a basis for the null space of A(q). Then each velocity vector
lies in the null space of A(q) for each q. If the rank of A(q) is equal to k, implying that the constraints are independent, then there will be an m = n − k-dimensional null space of A. Let {g1(q), …, gm(q)} be a basis for the null space of A(q). Then each velocity vector  satisfying Equation (14.8) can be expressed as
satisfying Equation (14.8) can be expressed as
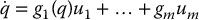
for suitable coefficients u1, …, um. Equation (14.14) specifies the allowable velocity vectors as a linear combination of the basis vectors g1, …, gm.
Example 14.4.
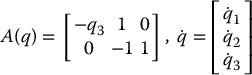
It is now easy to show by direct calculation that
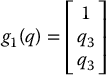
spans the one-dimensional null space of A.
Remark 14.1.
14.2 Involutivity and Holonomy
In this section we refine the notion of nonholonomic constraints that will be useful later when we discuss controllability of nonholonomic systems and Chow’s theorem.
Definition 14.3.
Given a set of Pfaffian constraints, as in Equation (14.8), let Ω be the codistribution spanned by the covectors {w1, …, wk} and let {g1, …, gm}, for m = n − k, be a basis for a distribution Δ satisfying

The vectors g1, …, gm then span the null space the matrix A defined previously. The distribution Δ is called the annihilator or annihilating distribution of Ω and is denoted Δ = Ω⊥. Conversely, Ω is the annihilating codistribution of Δ.
Theroem 14.1.
Suppose that Ω is the codistribution spanned by the covectors {w1, …, wk}. Then the set of constraints  is holonomic if and only if the distribution Δ = Ω⊥ is involutive.
is holonomic if and only if the distribution Δ = Ω⊥ is involutive.
Proof: Using the Lie derivative notation from Chapter 12, we can say that there exist functions hi, …, hk such that
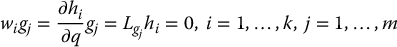
if and only if the constraints  are holonomic. From the Frobenius theorem the set of partial differential equations
are holonomic. From the Frobenius theorem the set of partial differential equations
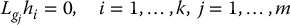
has a solution for h1, …, hk if and only if the distribution Δ is involutive, and the result follows.
Remark 14.2.
In the case of a single constraint  , the distribution Δ = span {g1, …, gn − 1} and involutivity of Δ is equivalent to Equation (14.5). At the other extreme, a set of n − 1 Pfaffian constraints for an n-dimensional system is always holonomic, since, in this case, Δ = span {g1}, which is always involutive.
, the distribution Δ = span {g1, …, gn − 1} and involutivity of Δ is equivalent to Equation (14.5). At the other extreme, a set of n − 1 Pfaffian constraints for an n-dimensional system is always holonomic, since, in this case, Δ = span {g1}, which is always involutive.
Example 14.5.
Consider again the constraint Equation (14.7) with w = ( − q3, 1, 0), which was shown to be nonholonomic. With Ω = span{w}, it is easy to see that a basis for the annihilating distribution Δ = Ω⊥ is
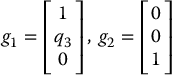
Computing the Lie Bracket [g1, g2] gives
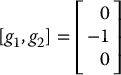
which is not a linear combination of g1 and g1. Hence, the distribution Δ is not involutive showing again that the Pfaffian constraint defined by w is nonholonomic.
Filtrations
Suppose now that the distribution Δ is not involutive. Then there is at least one pair of vector fields gi and gj in Δ such that the Lie Bracket [gi, gj] does not belong to Δ. Thus, with Δ1 = Δ = span{g1, …, gm}, we define Δ2 as the distribution
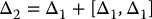
where
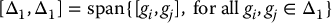
where [gi, gj] is the Lie Bracket of the vector fields gi and gj. The distribution Δ2 is spanned by all vectors gi ∈ Δ1 together with all possible vectors generated by taking Lie Brackets of pairs of vectors in Δ1. Thus, if Δ2 = Δ1 it simply means that the original distribution Δ is involutive.
If Δ1 is not involutive, then Δ2 ≠ Δ1 and its dimension is strictly larger than the dimension of Δ1. We can continue this process and define a sequence of distributions Δi, with Δ1 = Δ according to
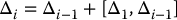
where
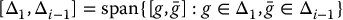
This sequence of distributions {Δi} is called a filtration associated with Δ.
Definition 14.4.
A filtration is said to be regular in a neighborhood U of q0 if
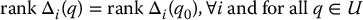
In other words, Δi has constant rank for all q.
If the filtration is regular then the dimension of Δi is greater than or equal to the dimension of Δi − 1 and cannot be greater than n, the dimension of the configuration space itself. If at some point there exists κ such that rank Δκ + 1 = rank Δκ then the above construction terminates. This leads us to
Definition 14.5.
Let {Δi} be a regular filtration associated with a distribution Δ. The smallest integer κ such rank Δκ + 1 = rank Δκ is called the degree of nonholonomy of the distribution Δ.
Note that m ⩽ rank Δκ ⩽ n and 1 ⩽ κ ⩽ n − m + 1. The degree of nonholonomy is related to the difficulty (or ease) of the motion planning and control problems. Based on the above derivation we can refine our definition of holonomic constraints as follows
Definition 14.6.
The set of k Pfaffian constraints, given by Equation (14.8), is
- Holonomic if κ = 1 or, in other words, if the dimension dim Δ1 = n
- Partially Nonholonomic if m < dim Δκ < n, i.e. 1 < κ < n − m + 1
- Completely Nonholonomic if dim Δκ = n, i.e. κ = n − m + 1
The distribution Δκ is called the involutive closure of Δ, denoted  , and by construction, is the smallest involutive distribution containing Δ, in the sense that if Δ′ is an involutive distribution such that Δ⊂Δ′, then
, and by construction, is the smallest involutive distribution containing Δ, in the sense that if Δ′ is an involutive distribution such that Δ⊂Δ′, then  .
.

Figure 14.2 The rolling disk.
14.3 Examples of Nonholonomic Systems
In this section we give examples of systems subject to nonholonomic constraints.
Example 14.6. (The Rolling Disk).
Figure 14.2 shows a disk rolling on a plane with its rolling axis parallel to the plane. The configuration of the disk can be defined by the variables q = (x, y, θ, rϕ), where x and y denote the Cartesian position of the ground contact point, θ denotes the heading angle, and ϕ denotes the angle of the wheel measured from the vertical. The rolling without slipping condition means that the instantaneous velocity of the ground contact point is zero, which implies
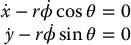
where r is the radius of the wheel. These constraints can be written as Pfaffian constraints in the form of Equation (14.3) with q = [x, y, θ, rϕ]T and
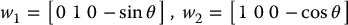
Since the dimension of the configuration space is n = 4 and there are two constraint equations, a basis for Ω⊥ will consist of two function g1, g2 orthogonal to w1, w2. It is easy to see that

are both orthogonal to w1 and w2. Thus, we can write a velocity vector  as
as
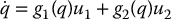
where u1 = v is the rate of rolling and u2 = ω is the turning rate.
We can now check to see if rolling without slipping constraints on the disk are holonomic or nonholonomic using Theorem 14.1. Computing the Lie brackets (Problem 14–3)
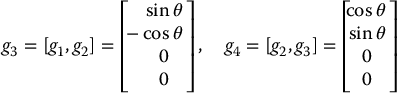
we see that

Therefore  . Thus the degree of nonholonomy is 3 and the constraints are completely nonholonomic.
. Thus the degree of nonholonomy is 3 and the constraints are completely nonholonomic.
Remark 14.3.
If we do not care about the orientation of the disk about the horizontal axis, i.e., if we ignore the last equation  , then the constraints in Equation (14.19) can be reduced to the single constraint
, then the constraints in Equation (14.19) can be reduced to the single constraint
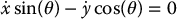
and we have a reduced-order model
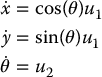
where
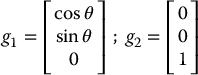
The system in Equation (14.23) is more commonly known as the unicyle model.
Example 14.7. (The Kinematic Car).
Figure 14.3 shows a simple representation of a car, or mobile robot, with steerable front wheels.s The configuration can be described by q = (x, y, θ, ϕ), where x and y are the point at the center of the rear axle, θ is the heading angle, and ϕ is the steering angle as shown in the figure. The rolling without slipping constraints are found by setting the sideways velocity of the front and rear wheels to zero. This leads to

which can be written as
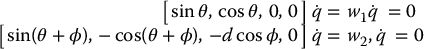
where the covectors w1 and w2 are
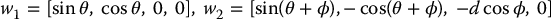

Figure 14.3 The kinematic car.
It is now straightforward to find vectors g1 and g2 orthogonal to w1 and w2 and write the corresponding system in the form of Equation (14.14). For example, we may take

Computing the Lie Brackets [g1, g2] and [g2, g3] gives
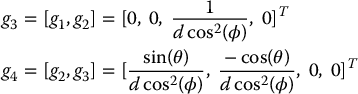
We have that

is involutive of rank 4. Hence the system has degree of nonholonomy κ = 3.
Example 14.8. (A Hopping Robot).
Consider the hopping robot in Figure 14.4. The configuration of this robot is defined by q = (ψ, ℓ, θ), where
| ψ | = | the leg angle |
| θ | = | the body angle |
| ℓ | = | the leg extension |

Figure 14.4 A hopping robot.
During its flight phase the hopping robot’s angular momentum is conserved. Letting I and m denote the body moment of inertia and leg mass, respectively, conservation of angular momentum leads to the expression

assuming the initial angular momentum is zero. This constraint may be written as  where
where  . Since the dimension of the configuration space is three and there is one constraint, we need to find two independent vectors, g1 and g2, spanning the annihilating distribution Δ = Ω⊥. It is easy to see that
. Since the dimension of the configuration space is three and there is one constraint, we need to find two independent vectors, g1 and g2, spanning the annihilating distribution Δ = Ω⊥. It is easy to see that
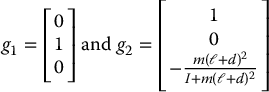
are linearly independent at each point and orthogonal to w. Checking involutivity of Δ we find that
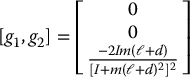
which is not a linear combination of g1 and g2. It follows that the constraint is nonholonomic and the degree of nonholonomy is κ = 2.
Example 14.9. (Differential Drive Robot).
The differential drive robot (henceforth, DDR) shown in Figure 14.5 consists of a chassis and two independently controlled wheels, giving it three degrees of freedom, x, y, and θ. The basic kinematic equations of the DDR are identical to those of the unicycle


Figure 14.5 The differential drive robot: top view (left), side view (right).
where v and ω are the linear and angular velocities of the chassis, respectively. Assume that each wheel has radius r and that the distance between the wheels is 2b. Assuming no wheel slipping, we can relate the chassis velocities v and ω to the left and right wheel velocities  and
and  as
as

Solving for v and ω gives
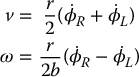
Note that actuating both wheels in the same direction with speed  results in a pure translation of the chassis with speed
results in a pure translation of the chassis with speed  while actuating both wheels in opposite directions with speed
while actuating both wheels in opposite directions with speed  results in a pure rotation with angular speed
results in a pure rotation with angular speed  .
.
Typically the wheels are actuated by DC-electric motors. Setting τR and τL as the left and right motor torques, respectively, we can express the dynamics of the DDR as
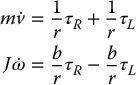
where m is the total mass of the DDR and J is its moment of inertia about the center of mass, which we can take as the midpoint of the wheel axle. With
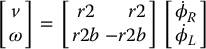
and
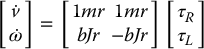
we have
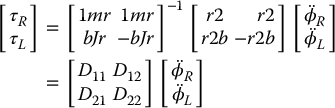
where  and
and  . If we include damping terms
. If we include damping terms  we can write the dynamic equations relating the motor torque to wheel acceleration as
we can write the dynamic equations relating the motor torque to wheel acceleration as

A typical DDR will be equipped with a low-level controller (usually PID control) to control the motor speed and position, which allows control of the wheel speed and position from Equation (14.31) assuming no wheel slipping. Thus, given desired linear and angular speeds, vd and ωd, of the chassis, one can assume that v = vd and ω = ωd after a short transient. Therefore, it is common just to use the kinematic equations (14.30) as the model for motion planning and control.
14.4 Dynamic Extension
Dynamic models for nonholonomic systems can be obtained in a straightforward way as an extension of the previous kinematic models. These extended models typically take the form
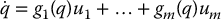

Note that the system in Equations (14.32)–(14.33) is now a system with drift of the form
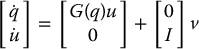
The above model can be derived from the Euler–Lagrange equations in the form

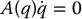
where  is defined using the nonholonomic Pfaffian constraints and λ is a vector of Lagrange multipliers. This model relates to the kinematic model
is defined using the nonholonomic Pfaffian constraints and λ is a vector of Lagrange multipliers. This model relates to the kinematic model
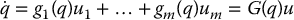
if we take, as before, g1, …, gm as a basis for the null space of A(q). Differentiating Equation (14.36) gives

Since GT(q)AT(q) = 0 by choice of basis vectors gi, if we substitute the expression for  from Equation (14.37) in into the Euler–Lagrange equations and multiply by GT(q) we obtain
from Equation (14.37) in into the Euler–Lagrange equations and multiply by GT(q) we obtain
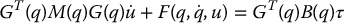
where
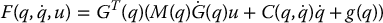
Assuming GT(q)B(q) is invertible, the control input τ can be chosen as a feedback linearizing control
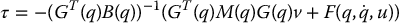
to obtain

Note that τ depends on the control input u since  . We can compute u from Equation (14.36) as
. We can compute u from Equation (14.36) as
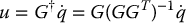
where G† is the right pseudoinverse of G, and substitute this expression into Equation (14.39) to complete the computation of the control τ.
Example 14.10.
For the unicycle model,

let τ1 be the driving force and τ2 be the steering torque so that
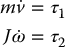
where m is the unicycle mass and J the moment of inertia about the vertical axis. Then a simple dynamic extension is given by

with ν1 = τ1/m and ν2 = τ2/J. To see how this model is obtained from the general theory, we can compute, using the above equations,
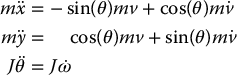
which we can write as
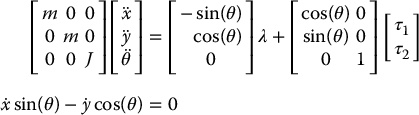
where the second equation above describes the nonholonomic constraint. Thus, with A and G given by

the above equations are of the form

and a straightforward calculation (Problem 14–10) gives
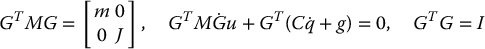
and therefore we obtain
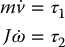
as above.
14.5 Controllability of Driftless Systems
In this section we consider the controllability of driftless systems of the form Equation (14.14). There are several notions of controllability for general nonlinear systems, all of which are equivalent for linear systems. The examples of wheeled mobile robots that we consider in this chapter all satisfy the strongest notion of controllability defined next and so we will not have need for other (weaker) notions of controllability.
We assume that the vector fields g1(q), …, gm(q) are smooth, complete,1 and linearly independent at each  . Under these conditions we can state the following:
. Under these conditions we can state the following:
Definition 14.7.
The driftless nonlinear system in Equation (14.14) is controllable if, for any q0 and q1  , there exists a time T > 0 and a control input
, there exists a time T > 0 and a control input

such that the solution q(t) of Equation (14.14) satisfies q(0) = q0 and q(T) = q1.
Let us digress for a moment to gain an intuitive understanding of the notion of nonlinear controllability and its relation to nonholonomy. Consider the familiar problem of parking a car. Referring to Figure (14.6) the desired motion is to move the car laterally, which is prohibited by the rolling constraints on the wheels. However, by sequentially applying the two control inputs, namely 1) turning the wheels left and right, and 2) driving forward and backward, one is able to park the car. With this example in mind, let the system

be defined by the two vector fields g1 and g2 and consider the following thought experiment consisting of sequentially applying the control u1 and u2:
- Set u1 = 1 and u2 = 0 and follow the vector field g1 for a time t = ε.
- Then set u1 = 0 and u2 = 1 to follow the vector field g2 for time ε < t ⩽ 2ε.
- Reverse the above by setting u1 = −1, u2 = 0 for time 2ε < t ⩽ 3ε.
- Finally, set u2 = −1 and u1 = 0 for time 3ε < t ⩽ 4ε.

Figure 14.6 The car parking problem.

Figure 14.7 Illustrating the notion of Lie bracket direction.
Denote by ϕgt(q0) the state of the system  at time t starting at q0 at time t = 0. The function ϕ is called the flow of the vector field g. With this notation, the state q(4ε) that is reached after the above thought experiment is given by
at time t starting at q0 at time t = 0. The function ϕ is called the flow of the vector field g. With this notation, the state q(4ε) that is reached after the above thought experiment is given by
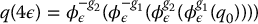
It is shown in most basic texts in differential geometry using a Taylor series expansion of the flow that the resulting state reached after the four sequential moves is given by
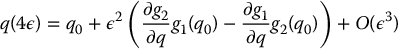
In other words, the motion is equivalent, for small ε, to moving in the Lie bracket direction [g1, g2]. We will show later that the lateral motion of the car is precisely the direction given by the Lie bracket of the ‘turning’ and ‘driving’ input vectors.
The above discussion suggests that the possible directions of motion, i.e., the velocity directions, include not only the directions given by g1, …, gm but also motions in the direction [gi, gj], [gk, [gi, gj]], and so on. Thus, it is important to know if the vectors [gi, gj] are simply linear combinations of the original vectors g1, …, gm or if they are vectors defining new and independent directions.
The next result, known as Chow’s theorem, formalizes this notion and gives a necessary and sufficient condition for a system given by Equation (14.43) to be controllable.
Theroem 14.2. (Chow).
The driftless system

is controllable if and only if  at each
at each  , where
, where  is the involutive closure of Δ(q) = span{g1(q), …, gm(q)}.
is the involutive closure of Δ(q) = span{g1(q), …, gm(q)}.
The condition  is called the controllability rank condition. The involutive closure
is called the controllability rank condition. The involutive closure  of Δ is also called the control Lie algebra for the system in Equation (14.43).
of Δ is also called the control Lie algebra for the system in Equation (14.43).
Example 14.11.
Consider the following system on 
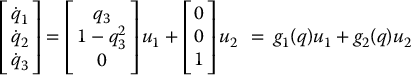
with three states q1, q2, q3, and two control inputs, u1 and u2. It is easy to see that the distribution Δ = span{g1, g2} has rank two for all values of  . The Lie bracket [g1, g2] is
. The Lie bracket [g1, g2] is
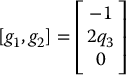
and, therefore, we have

for all values of  . Therefore, by Chow’s theorem, the system is controllable on
. Therefore, by Chow’s theorem, the system is controllable on  .
.
Remark 14.4.
It is apparent from Chow’s theorem and our definition of nonholonomy that a driftless system with  and
and  is controllable if and only if the constraints are completely nonholonomic, which means that the degree of nonholonomy κ should be κ = n − m + 1. The reader should now check that each of the examples that we presented in Section 14.3 is controllable according to Chow’s theorem. Table 14.1 summarizes this result.
is controllable if and only if the constraints are completely nonholonomic, which means that the degree of nonholonomy κ should be κ = n − m + 1. The reader should now check that each of the examples that we presented in Section 14.3 is controllable according to Chow’s theorem. Table 14.1 summarizes this result.
Table 14.1 Examples of controllable driftless systems.
| Example | n | m | κ |
| rolling disk | 4 | 2 | 3 |
| unicycle | 3 | 2 | 2 |
| kinematic car | 4 | 2 | 3 |
| hopper | 3 | 2 | 2 |
14.6 Motion Planning
We have given several examples of nonholonomic mobile robots that are controllable according to Chow’s theorem. Chow’s theorem tells us when a driftless system is controllable but does not tell us how to find the control input to steer the system from a given initial state x0 to a desired final state x1. In this section we present several ideas for planning feasible trajectories for these systems.
14.6.1 Conversion to Chained Forms
We have seen the usefulness of transforming systems into canonical or normal forms through the use of nonlinear coordinate transformations and nonlinear feedback, as in the feedback linearization in Chapter 12 and partial feedback linearization in Chapter 13. In this section we introduce the so-called chained form which gives a useful transformation of the kinematics of many nonholonomic systems. We limit the discussion to systems with two inputs, such as the unicycle, DDR, and kinematic car.
Example 14.12.
To motivate the subsequent development, consider again the unicycle model
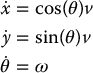
Define a coordinate transformation

Note that the coordinates (z2, z3) represent a rotational transformation of (x, y) through the angle θ. In terms of the transformed coordinates, z1, z2, and z3, the input transformation
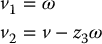
results in the system (Problem 14–5)
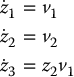
which is referred to as a (2, 3)-chained system since it has two inputs and three states.
We note that, like the unicycle model it derives from, Equation (14.44) defines a driftless nonlinear system, and can be shown to be controllable using Chow’s theorem (Problem 14–12).
In the system of equations (14.44) the variables z1 and z2 are called base variables and can be independently controlled with inputs v1 and v2, respectively. The third coordinate z3 is called a fiber variable and evolves according to the input z2v1 and therefore cannot be independently controlled.
Steering Using Sinusoids
The chain form representation is useful for deriving trajectories in configuration space using several methods. One such method is to use sinusoidal functions at different frequencies for the inputs v1 and v2 to move the shape variables through periodic motions. This will move the fiber variables to new values that are functions of the amplitudes and frequencies of the input functions. The motion planning problem then becomes one of choosing appropriate values for the amplitudes and frequencies of v1 and v2. We illustrate this idea below for the case of the unicycle model.
Example 14.13.
Consider the chained-form system derived above from the unicycle model
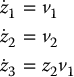
and let us choose the control inputs v1 and v2 to minimize the quadratic cost function
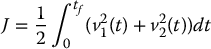
To solve this problem we form the Hamiltonian function
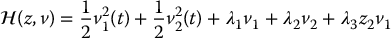
where the Lagrange multiplier vector λ = (λ1, λ2, λ3) satisfies the adjoint equations  . Since the Hamiltonian
. Since the Hamiltonian  is independent of z1 and z3, the adjoint equations are easily computed as
is independent of z1 and z3, the adjoint equations are easily computed as

The necessary condition for optimality,  , leads to
, leads to
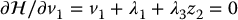
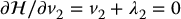
from which we get

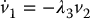

which has the general solution

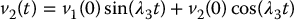
Thus, we have shown that the control for the chained-form system that minimizes the cost function (1.46) consists of sinusoidal inputs.
This result leads to the following motion planning strategy for the above system:
- First, use any method to move the base variables z1 and z2 to their desired final values, zd1 and zd2, respectively. Since the base variables are independently controlled, this step is simple and should be completed in finite time t1.
- Next, execute a periodic motion of the base variables over one period T. This motion will bring the base variables back to their desired final value and move the fiber variable z3 from z3(t1) to z3(t1 + T). Choose the periodic motion of the base variables so that z3(t1 + T) = zd3, the desired value for z3.
The strategy is suboptimal since the control of the shape variables in the first step is not necessarily optimal. If we now choose the controls v1 and v2 as
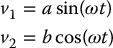
it is easily shown (Problem 14–8) that after 2π/ω seconds, z1 and z2 return to their initial values whereas the change in z3 is abπ/ω2.
Example 14.14.
Suppose that we wish to move the unicycle from the origin (z1, z2, z3) = (0, 0, 0) to (x1, x2, x3) = (0, 0, 10) in two seconds. Using the above controls with a = π, ω = π, b = 10 results in the response shown in Figure 14.8.

Figure 14.8 Response of z1, z2, and z3: Note that z1 and z2 return to their original values after 2 seconds while z3 moves from the origin to z3 = 10 as desired.
Chained Form for Higher Dimensional Systems
We can generalize the previous idea of conversion to chained form to higher dimensional (2, n)-chained form systems as follows.
Definition 14.8.
A (2, n) chained-form is a driftless system with 2 inputs, v1 and v2, and n configuration variables z1, …, zn in the form

In this case, z1 and z2 are the base variables and z3, …, zn are the fiber variables.
The system in Equation (14.55) can be written in the form of a driftless system as

where
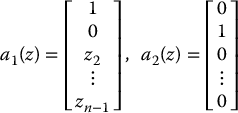
It is not too difficult to show that the chained-form system, Equation (14.55), is controllable according to Chow’s theorem. In order to see this, one can show by induction (Problem 14–6) that
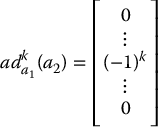
where the non-zero entry (−1)k appears in the k + 2 position. It follows by direct calculation that the distribution
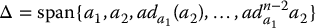
has dimension n and controllability follows from Chow’s theorem.
We state without proof a sufficient condition for the two-input case for conversion to chained form. Specifically, given a driftless system of the form
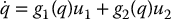
there exist a diffeomorphic change of coordinates  and a control input v = β(u) that transforms Equation (14.57) into the (2, n) chain form Equation (14.55) if the following distributions are constant rank and involutive
and a control input v = β(u) that transforms Equation (14.57) into the (2, n) chain form Equation (14.55) if the following distributions are constant rank and involutive
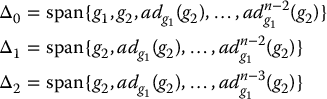
and there exists a function h1(q) such that

and a function h2, independent of h1, such that

Note that Equations (14.59) and (14.60) are a set of partial differential equations that must be solved to find h1 and h2. The required change of coordinates in the state and control inputs are then given by
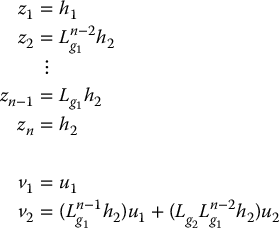
Example 14.15.
We can apply the above transformation to the kinematic car

It is straightforward (Problem 14–7) to compute the distributions Δ0, Δ1, and Δ2 and verify that they are of constant rank and involutive. With h1 = q1 and h2 = q2 the state transformation
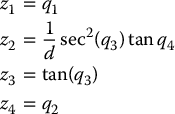
and input transformation
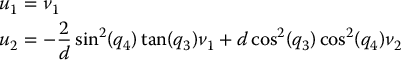
yields the required (2, 4) chain system.
For the (2, n) chained-form system, Equation (14.55), a similar procedure to the above can be applied to sequentially move each variable zk to its desired value as follows:
- First choose v1 and v2 to move the base variables z1 and z2 to their desired values in time t1. As before, the fiber variables z3, …, zn will move to new values z3(t1), …, zn(t1).
- For 3 ⩽ k ⩽ n, steer zk to its desired value zdk with controls
over one period, T = 2π/ω, where a and b are chosen to satisfy

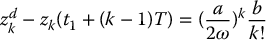
Carrying out the sequential steering controls moves the chained-form system from z0 to zd in time t = t1 + (n − 2)T.
Example 14.16.
Consider the (2, 4) chained-form system

and suppose we wish to move the states from (0, 0, 0, 0) to (0, 0, 10, 15) in 4 seconds. In the first stage we take v1 and v2 as in the previous example as
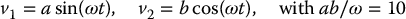
After 2 seconds, z3 reaches its desired value of 10 and z4(2) = −10. In the second stage we take
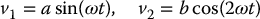
with  . With zd4 = 15 and a = ω = π, this gives b = 100. The responses are shown in Figure 14.9.
. With zd4 = 15 and a = ω = π, this gives b = 100. The responses are shown in Figure 14.9.

Figure 14.9 Response of z1, z2 and z3.
14.6.2 Differential Flatness
In this section we introduce the notion of differential flatness and its application to the motion planning and control problems. The property of flatness simplifies the process of determining feasible trajectories for mechanical systems. This is particularly useful for underactuated systems and systems with nonholonomic constraints since, as we have seen, not all trajectories are feasible. It turns out that all of the systems considered in the chapter, indeed all driftless systems that can be converted to chained form, are differentially flat.
The basic idea of differential flatness is, given a system with n states and m inputs, find a set of m outputs so that the states and inputs can be expressed as functions of these m outputs and their derivatives. More precisely, we have
Definition 14.9.
The nonlinear system
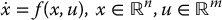
is said to be differentially flat if there exists an output y = (y1, …, ym), with the same dimension as the control input, satisfying the following conditions:
- There exists a nonnegative integer α such
 for each i = 1, …, m, for some smooth functions h1, …hm.
for each i = 1, …, m, for some smooth functions h1, …hm. - There are smooth functions, ϕ, and ψ, and a nonnegative integer r ⩾ 0 such that
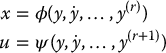
- The components yi of y are differentially independent in the sense that they satisfy no differential equation of the form
 .
.
The components of the vector y in the above definition are called flat outputs. In other words, once a suitable set of flat outputs is identified, the state x and input u of the system are completely determined as functions of the flat outputs and their derivatives. Specifically, for every sufficiently differentiable curve t → y(t), there corresponds a trajectory

The proof of this property is beyond the scope of this text. In the control field, the notion of differential flatness grew out of work on static and dynamic feedback linearization and is intimately related to these latter concepts.
Remark 14.5.
It is routine to show that any system that can be transformed to the Brunovsky form in Equation (12.35) is flat. This includes controllable linear systems as well as nonlinear systems that are feedback linearizable (Problem 14–13).
For the problem of trajectory tracking, suppose that we want to find a feasible trajectory with initial and final conditions given as (t0, x(t0), u(t0)), and (tf, x(tf), u(tf)), respectively. Then, we can calculate corresponding values  and
and  for the flat outputs with s ⩽ r. We can then interpolate a smooth curve t → y(t) between these initial and final values, which then determines the trajectory t → (x(t), u(t)) between t0 and tf. By construction, the computed trajectory automatically satisfies the system equations and hence any constraints, nonholonomic or otherwise.
for the flat outputs with s ⩽ r. We can then interpolate a smooth curve t → y(t) between these initial and final values, which then determines the trajectory t → (x(t), u(t)) between t0 and tf. By construction, the computed trajectory automatically satisfies the system equations and hence any constraints, nonholonomic or otherwise.
Example 14.17.
For the DDR system, a set of flat outputs is given by y1 = x, y2 = y. The remaining variables are then

Suppose that we want to move the DDR from configuration (x, y, θ) = (0, 0, 0) at time t0 = 0 to (x, y, θ) = (10, 10, 0) at time tf = 1. Then, in terms of the flat outputs, the constraints are
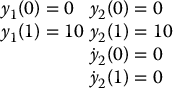
where the last two constraints on  indicate that the orientation θ of the DDR is horizontal at the beginning and end of the trajectory. Since there are two constraints on y1 and four constraints on y2, we can choose reference trajectories as polynomials of the form
indicate that the orientation θ of the DDR is horizontal at the beginning and end of the trajectory. Since there are two constraints on y1 and four constraints on y2, we can choose reference trajectories as polynomials of the form
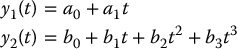
Solving for the polynomial coefficients using the given constraints yields
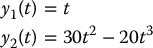
Figure 14.10 shows the resulting trajectory and control inputs.

Figure 14.10 Trajectory and control inputs of the DDR computed from the flat outputs.
In general, determining when a given system is flat and finding a set of flat outputs is difficult. However, it is known that the (2, n) chain-form system is always flat with flat outputs y1 = z1 and y2 = zn.
Example 14.18.
For the chain-form system below, a set of flat outputs
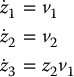
is y1 = z1 and y2 = z3. Then it is straightforward to show that the remaining variables z2, v1, v2 are given by
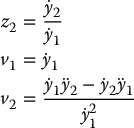
14.7 Feedback Control of Driftless Systems
In this section we consider the problem of finding feedback control laws, as opposed to the purely time-based, open-loop controllers that we derived in the previous section. We consider both the problem of pose regulation, i.e., point-to-point motion, and the problem of trajectory tracking. The first result below, known as Brockett’s theorem, gives a necessary condition for the existence of a smooth stabilizing control.
14.7.1 Stabilizability
Theroem 14.3. (Brockett).
Given the nonlinear system
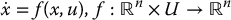
with f(x, u) continuously differentiable and f(0, 0) = 0, suppose that there exists a continuously differentiable (smooth) feedback control law u = u(x) that makes the origin x = 0 asymptotically stable. Then the image of the map f contains a neighborhood of the origin.
Example 14.19.
For the system
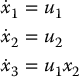
It is easily seen that, given any a ≠ 0, there does not exist (x, u) satisfying
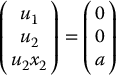
Thus, the image (range) of the function f does not contain a neighborhood of the origin and so there does not exist a smooth C1 feedback control law u(x) that stabilizes the origin.
Most nonholonomic systems, including the examples considered in this chapter, do not satisfy Brockett’s necessary condition for the existence of a smooth stabilizing feedback control. As a result, Brockett’s theorem has motivated a great deal of research into finding alternative control schemes for more general nonholonomic systems. These include
- Open-loop control laws
- Time-varying control laws u = u(x, t)
- Discontinuous and switching control laws
Example 14.20.
Consider the unicycle system. It is easy to see that for any initial condition x0, y0, θ0, the following switching control scheme drives the system to the origin, i.e. is a stabilizing control:
- Rotate the unicycle in place to line up the orientation with the origin
- Translate until (x, y) = (0, 0)
- Rotate in place until θ = 0
We note that if the nonlinear system  is linearly controllable, then there is always a smooth feedback control law, in fact, of the form u = −kx, that stabilizes the origin locally.
is linearly controllable, then there is always a smooth feedback control law, in fact, of the form u = −kx, that stabilizes the origin locally.
Example 14.21.
Consider the Acrobot model
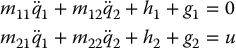
and suppose that g1 = 0. From Proposition (13.1) we know that this system is not linearly controllable about the origin. It is left as an exercise (Problem 14–9) to show that there is no smooth feedback control that stabilizes the origin.
14.7.2 Nonsmooth Control
One way to circumvent the obstruction due to Brockett’s theorem is to use discontinuous or switching control.
Sliding-Mode Control
The possibility of using discontinuous control to circumvent the obstruction imposed by Brockett’s theorem suggests the application of sliding-mode control. Consider the chain-form system
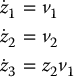
Define σ = z3 − z1z2/2 and let the controls v1 and v2 be given as

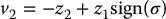
We want the manifold σ = 0 to serve as a sliding surface for the system trajectory. Let V be given as
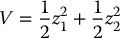
Then

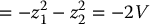
Thus, V(t) = V(0)e− 2t → 0 as t → ∞ and therefore z1(t) and z2(t) converge asymptotically to zero. With the given choice of σ a straightforward calculation shows
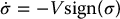
Therefore, |σ(t)| is nonincreasing. If σ(t) reaches the origin at some time t = T it will remain at the origin and slide along the surface z3 = z1z2/2 toward the origin. Figures (14.11) and (14.12) shows a simulation of this controller.

Figure 14.11 Sliding-mode control of the DDR in chain form: response of the chain variables and the sliding variable σ.

Figure 14.12 Sliding-mode control of the DDR in chain form: control inputs.
Dynamic Extension
For systems like the unicycle or DDR, it may be difficult to implement such a sliding-mode controller that requires rapid switching of the velocities v and ω. For this reason we may consider the dynamic extension
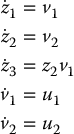
For example, u1 and u2 could represent the torque inputs, which we can take as

where we choose
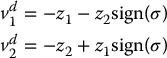
as reference trajectories for v1 and v2. This will have the effect of smoothing the control signals and is a more practical control from the standpoint of implementation. Figures (14.13) and (14.14) show the responses with the modified controls.

Figure 14.13 Modified sliding-mode control of the DDR in chain form: response of the chain variables and the sliding variable σ

Figure 14.14 Modified sliding-mode control of the DDR in chain form: control inputs.
14.7.3 Trajectory Tracking
Lyapunov Design
In this section we illustrate the use of Lyapunov-like design for pose regulation of the DDR robot. Considering the DDR model
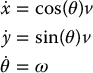
let us first change to polar coordinates (r, ϕ) by setting

and define β = ϕ − θ. In terms of coordinates r, β, and ϕ a straightforward computation gives
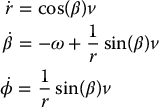
Note that Equation (14.70) is only valid on R3 − {0} because of the singularity at r = 0. Thus, the assumptions of Brockett’s prohibiting the design of a smooth stabilizing control law do not hold. Define a candidate Lyapunov function
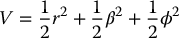
Then,  satisfies
satisfies
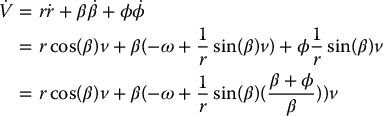
If we set the controls v and ω as
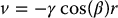
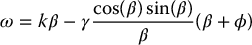
a straightforward calculation shows that
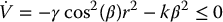
Due to the singularity at r = 0, some additional care must be taken to conclude that the trajectory of the system converges asymptotically to the origin. We note that Equations (14.71) and (14.74) together imply that all solutions are bounded and that  asymptotically. Moreover, r does not reach zero in finite time due to the boundedness of β and the expression for
asymptotically. Moreover, r does not reach zero in finite time due to the boundedness of β and the expression for  . An application of Barbalat’s Lemma (see Appendix C) now implies that all trajectories asymptotically converge to the origin.
. An application of Barbalat’s Lemma (see Appendix C) now implies that all trajectories asymptotically converge to the origin.
Example 14.22.
Suppose we want to move the DDR from the initial pose (x, y, θ) = (− 1, 1, 3π/4) to the origin. The corresponding initial conditions for the transformed coordinates (r, β, ϕ) are  . Figure 14.15 shows the path computed using the above procedure.
. Figure 14.15 shows the path computed using the above procedure.

Figure 14.15 DDR pose regulation.
14.7.4 Feedback Linearization
In this section we present the application of feedback linearization for the problem of trajectory tracking for mobile robots. Thus, instead of pose regulation, we want the system configuration to follow a time-varying trajectory. With regard to static feedback linearization, the driftless system

is feedback linearizable in a neighborhood  of q0 if and only if rank G(q) = n in
of q0 if and only if rank G(q) = n in  . This requires the system to be fully actuated, i.e. m = n, in which case the distribution
. This requires the system to be fully actuated, i.e. m = n, in which case the distribution
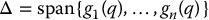
is trivially involutive and a feedback linearizing control is given by
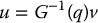
In the more interesting underactuated case m < n we may apply the method of partial or input/output linearization to try to linearize m degrees of freedom. In this case, the problem is to determine a suitable output with respect to which a linear input/output relation can be established.
Example 14.23.
Consider again the differential drive robot
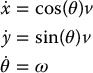
and suppose that we choose the outputs

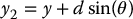
with d ≠ 0. The outputs are the coordinates of the point d shown in Figure 14.16. We can take d positive if it is located ahead of the wheel axle and negative otherwise. Differentiating the outputs gives
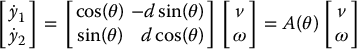

Figure 14.16 Differential drive robot showing the location of the output located d units ahead of the wheel axle.
The matrix A is invertible for d ≠ 0 and the input transformation
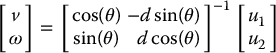
results in
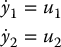
Using the expression for ω from Equation (14.82) yields the 3-dimensional normal form

Thus, given a desired output trajectory (yd1(t), y2d(t)), which is really a desired trajectory for the point d to follow, the control input

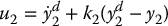
results in exponential tracking of the output trajectory. Note that the zero dynamics are given by the equation

Figure 14.17 shows a simulation of the above controller with reference trajectory
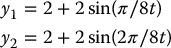
The initial conditions were chosen as (0, 0, 0) with d = 0.1.

Figure 14.17 Trajectory of the differential drive robot with partial feedback linearization control.
Dynamic Feedback Linearization
The above method of input/output linearization fails for d = 0. To have the (x, y) coordinates track desired reference trajectories, we will use the method of dynamic feedback linearization, which we have so far not considered in any applications. To understand this design method, we consider the differential drive robot

with output equations
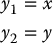
Differentiating the outputs gives
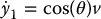
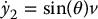
Differentiating the outputs a second time would result in the derivative of v appearing in the equations, which we want to avoid. Therefore, we let v be represented as a new state variable ξ = v. Then  , the linear acceleration. Now, if we differentiate Equations (14.87)–(14.88) with respect to time we get
, the linear acceleration. Now, if we differentiate Equations (14.87)–(14.88) with respect to time we get
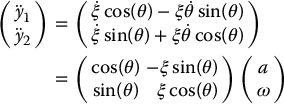
Thus, we can take
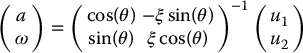
which results in
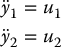
as long as ξ ≠ 0. Given a desired output trajectory (yd1(t), y2d(t)) we can set
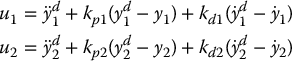
and the tracking errors ei = yi − ydi satisfy
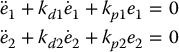
and exponentially convergence to zero. The resulting dynamic compensator is given by
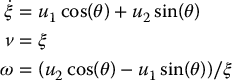
Note that the angular velocity ω in Equation (14.89) is unbounded as the linear velocity ξ tends to zero. This means that the dynamic feedback linearization approach requires that the robot never stop moving and, hence, this method cannot be used for pose regulation.
14.8 Chapter Summary
This chapter provided an introduction to the control of nonholonomic systems with particular emphasis on wheeled mobile robots. We provided examples and case studies for several models including the unicycle, differential drive robot and a car-like robot. All of these systems are modeled as driftless systems of the form

with n configuration variables and m < n control inputs.
Nonholonomic Systems
We introduced the notion of nonholonomic systems, which has applications in mobile robots, hopping robots, gymnastic robots, and other systems that are subject to either rolling without slipping constraints or conservation of momentum constraints. The importance of nonholomomic constraints is that controllability is possible even though the systems are underactuated and not linearly controllable. The concept of involutive closure of the distribution Δ = span {g1, …, gm} is the key concept to understand controllability of driftless systems.
Controllability and Stabilizability
We introduced two important control results, namely Chow’s theorem and Brockett’s theorem. Chow’s theorem states that a driftless system is completely controllable if and only if the involutive closure  of the above distribution Δ has full rank n. Brockett’s theorem states that, for the driftless systems considered here, there does not exist a continuously differentiable, time-invariant feedback control law to steer the system to the origin. Thus, one has to consider alternative control strategies, such as open-loop control, time-varying feedback control, or switching control.
of the above distribution Δ has full rank n. Brockett’s theorem states that, for the driftless systems considered here, there does not exist a continuously differentiable, time-invariant feedback control law to steer the system to the origin. Thus, one has to consider alternative control strategies, such as open-loop control, time-varying feedback control, or switching control.
Motion Planning
With regard to open-loop strategies to control driftless systems, we showed that most of the systems of interest can be transformed into chained form, which is a particularly useful canonical form for motion planning. We illustrated the idea of steering using sinusoids to generate feasible motions for stabilization. We also showed that the systems considered in this chapter are examples of systems that are differentially flat, which also simplifies the motion planning and trajectory generation problems.
Feedback Control
We presented several feedback control strategies for regulation and tracking, in particular Lyapunov-based design, sliding-mode control, input/output linearization, and dynamic feedback linearization.
Problems
- Verify that the only solution for γ to the equations in Example 14.41 is γ = 0.
- Verify that the constraint
 in Equation (14.11) can be integrated to
in Equation (14.11) can be integrated to  and
and  .
. - Fill in the details in Example 14.1 showing that the constraints are nonholonomic.
- Fill in the details in Example 14.6 necessary to derive the vector fields g1 and g2 and show that the constraints are nonholonomic.
- Verify the calculations given in Example 14.7 that transform the DDR model into chain form.
- Show by induction that the (2, n) chained-form system in Equation (14.55) is controllable.
- Compute the distributions Δ0, Δ1, and Δ2 in Example 14.15 and verify that they are of constant rank and involutive.
- Carry out the details to verify the claim in Example 14.21 that the variables z1 and z2 return to their initial values after 2π/ω seconds and the change in z3 is abπ/ω2.
- Show, using Brockett’s theorem, that there does not exist a smooth stabilizing feedback control for the Acrobot model in Example 14.21 if g1 = 0.
- Verify the calculations in Example 14.10.
- Consider the two-link planar RR robot

Investigate the existence of a smooth stabilizing control law under various scenarios regarding u1, u2, g1, g2. - Use Chow’s theorem to show that the system defined by Equation (14.44) is controllable.
- Let
 be a single-input nonlinear system and suppose that the system is feedback linearizable with a nonlinear change of coordinates and nonlinear feedback. Show that the system is differentially flat.
be a single-input nonlinear system and suppose that the system is feedback linearizable with a nonlinear change of coordinates and nonlinear feedback. Show that the system is differentially flat.
Notes and References
A more complete treatment of the control of nonholonomic systems, including mobile robots, can be found in [118] and [32]. An excellent introduction to the topics here is [100], which gives examples of underactuated planar manipulators in addition to wheeled mobile robots. Another good tutorial on the topic of nonholonomic control is [80]. Additional references on nonholonomic behavior and control of planar manipulators are [130, 101, 102].
Our treatment of systems in chained form follows closely the development in [118] and [100]. The treatment of steering using sinusoids follows [121] and [118]. A proof of Brockett’s theorem is in [18]. An excellent treatment of switching control is [95]. Additional details on differential flatness and its application to nonholonomic motion planning is in [120, 141]. The Lyapunov-like approach to control of the unicycle using polar coordinates is taken from [3]. More details on the concept of dynamic extension can be found in [13, 80]. Dynamic feedback linearization is treated in [99, 101, 22].
Note
- 1 A complete vector field is one for which the solution of the associated differential equation exists for all time t.
 . We can write these as
. We can write these as  where
where
 when the control inputs u1, …, um are zero. In many systems of interest the coefficients ui in Equation (
when the control inputs u1, …, um are zero. In many systems of interest the coefficients ui in Equation (