CHAPTER 13
UNDERACTUATED ROBOTS
13.1 Introduction
In this chapter we consider the control of an important class of robots known as underactuated robots. By an underactuated robot, or more generally an underactuated mechanical system, we mean one in which the number of independent control inputs is fewer than the number of generalized coordinates.
Underactuation arises in several ways, for example, from intentional design as in the so-called Acrobot and Pendubot described below, in which one or more of the joints are unactuated, or it may arise because of the mathematical model used for control design, such as when joint flexibility is included in the model. In the previous chapter we discussed the control of n-link flexible-joint robots, which have 2n degrees of freedom and n control inputs and hence fall into the class of underactuated robots.
Systems with unilateral constraints or nonholonomic constraints are also often underactuated. For example, in legged locomotion, the contact between the foot and the ground represents a unilateral constraint and is unactuated. Walking robots are therefore inherently underactuated. Wheeled robots, swimming robots, space robots, and flying robots are all examples of underactuated robots.
The class of underactuated robots is thus large and complex and the control problems are more difficult than for fully-actuated robots. As we saw in previous chapters, fully actuated robots possess a number of strong properties that facilitate control design. In particular, fully-actuated manipulator arms are globally feedback linearizable. This is generally not true for most underactuated systems, flexible-joint robots being an exception. As a result, the control problems for underactuated systems often require the development of new tools for controller design.
We will present modeling and control results in this chapter for a specific class of robots that includes underactuated serial-link robots. The tools we will use include partial feedback linearization, switching control, and energy/passivity methods. In Chapter 14 we will present additional control results for nonholonomic mobile robots.
13.2 Modeling
Figure 13.1 shows an underactuated serial-link robot. The shaded joints represent actuated degrees of freedom and the unshaded joints represent unactuated degrees of freedom. We assume that there are n joints with m ⩽ n of the joints actuated and the remaining n − m joints unactuated. The actuated degrees of freedom are called active joints and the unactuated degrees of freedom are called passive joints. The difference ℓ = n − m is called the degree of underactuation.

Figure 13.1 An underactuated serial-link robot.

Figure 13.2 Upper-actuated (left) and lower-actuated (right) robots.
Upper-Actuated and Lower-Actuated Models
It is convenient for later analysis and control design to model the robot, by renumbering the joint variables if necessary, as either upper-actuated or lower-actuated as we define next.
Definition 13.1.
An upper-actuated system is one in which the first m, or proximal, joints are active and the remaining ℓ = n − m, or distal, joints are passive.
A lower-actuated system is one in which the last m joints are active and the first ℓ = n − m joints are passive.
Note that the terms upper and lower refer to the analogy to upper and lower arms rather than the joint numbers. This will become more clear in the examples that follow.
The dynamic equations of motion of a general n-DOF underactuated system can be derived using the tools from Chapter 6 and expressed as
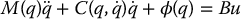
where M(q) is the n × n inertia matrix,  is the Coriolis and centrifugal matrix and the vector ϕ(q) contains the generalized forces derived from the potential energy, such as the gravitational forces and elastic forces, if present. For simplicity, we will ignore the actuator dynamics and take the inertia matrix M(q) to be identical to the matrix D(q) as defined in Chapter 6.
is the Coriolis and centrifugal matrix and the vector ϕ(q) contains the generalized forces derived from the potential energy, such as the gravitational forces and elastic forces, if present. For simplicity, we will ignore the actuator dynamics and take the inertia matrix M(q) to be identical to the matrix D(q) as defined in Chapter 6.
The matrix B is an n × m matrix of rank m reflecting the fact that there are m independent actuators. For simplicity we take the matrix B = Bu for an upper-actuated robot and B = Bl for a lower-actuated robot, as
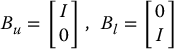
where I is the m × m identity matrix and 0 is an ℓ × m matrix of zeros.
With the vector  of generalized coordinates partitioned as q = (q1, q2) with
of generalized coordinates partitioned as q = (q1, q2) with  and
and  , we write the dynamic equations of a lower-actuated system as
, we write the dynamic equations of a lower-actuated system as
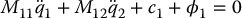
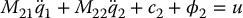
where
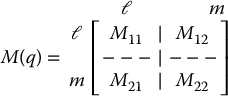
is a partition of the symmetric, positive definite inertia matrix into blocks
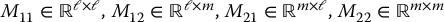
the vectors  and
and  contain Coriolis and centrifugal terms,
contain Coriolis and centrifugal terms,  and
and  are derived from the potential energy, and
are derived from the potential energy, and  represents the input generalized forces at the active joints.
represents the input generalized forces at the active joints.
Likewise, with a similar partitioning of the generalized coordinates q = (q1, q2) with  and
and  and similar partitioning of M(q),
and similar partitioning of M(q),  , and ϕ(q) the dynamics of an upper-actuated system can be written as
, and ϕ(q) the dynamics of an upper-actuated system can be written as
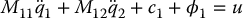
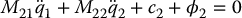
In this case, the sub-blocks of the inertia matrix have dimensions shown below.
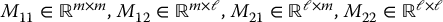
and also  ,
,  ,
,  , and
, and  .
.
Second-Order Constraints
Since the right-hand side of Equation (13.2) (or (13.6)) is equal to zero, this equation in effect defines constraints on the generalized coordinates. In particular, any reference trajectory  must satisfy (13.2) (or(13.6)). Hence underactuated robots cannot track arbitrary trajectories, which is another important difference between fully-actuated and underactuated robots.
must satisfy (13.2) (or(13.6)). Hence underactuated robots cannot track arbitrary trajectories, which is another important difference between fully-actuated and underactuated robots.
Example 13.1.
Recall the flexible-joint robot model from Chapter 12
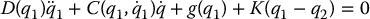
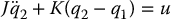
which is in the lower-actuated form (13.2)–(13.3) with M11 = D(q1), M12 = M21 = 0, M22 = J,  , c2 = 0, ϕ1 = g(q1) + K(q1 − q2), and ϕ2 = K(q2 − q1).
, c2 = 0, ϕ1 = g(q1) + K(q1 − q2), and ϕ2 = K(q2 − q1).
In this form, it is straightforward to show that the control input u can be designed so that the motor angle q2(t) follows a desired motor angle trajectory qd2(t). The resulting motion of the link angle q1(t) will then be determined by Equation (13.7).
Alternatively, as we showed in Chapter 12, this system is globally feedback linearizable in the state coordinates y1, …, y4 with y1 = q1, the vector of link angles, and y2, y3, y4 successive derivatives of y1. In these coordinates, any desired trajectory yd1(t) = q1d(t) can be tracked but no independent trajectory for the motor angles q2 can be tracked. Rather, the resulting trajectory for q2 is determined implicitly by the trajectory for q1 and Equation (13.8). In either case, a desired trajectory may be specified for one, but not both, of the generalized coordinates.
13.3 Examples of Underactuated Robots
13.3.1 A Note About Angle Convention
In this section we give several examples of underactuated systems that we will use to illustrate various theoretical concepts and control design methods. Referring to Figure 13.3 we first note that the dynamic equations of motion that we derived in Chapter 6 used the DH convention for the joint angles q1 and q2 shown in (a). With a few exceptions, we will follow this convention throughout the present chapter. Depending on the context, other conventions such as (b), (c), or (d) are also used in books and research articles. The reader should note the particular convention used in each example.

Figure 13.3 Illustrating common reference angle conventions.
13.3.1 The Cart-Pole System
The cart-pole system or inverted pendulum on a cart, shown in Figure 13.4, is a classic example used to illustrate nonlinear dynamics and test various control strategies. The inverted pendulum is representative of several practical systems and applications. The overhead crane transporting a load can be modeled as a cart-pole system. In this case, the control challenge is to transport the load while minimizing the pendular swing motion of the load, referred to as sway. The pitch dynamics of a rocket ascending vertically with gimballed thrust is similar to an inverted pendulum. Fuel slosh in the tanks also exhibits pendulum-like dynamic behavior. Likewise, the inverted pendulum is often used as a simple model to study problems of balance and walking in bipedal locomotion. Figure 13.5 illustrates these examples of pendulum-like dynamics.

Figure 13.4 The inverted pendulum on a cart.

Figure 13.5 An overhead crane, a gimballed rocket and bipedal walking as examples of the inverted pendulum.

Figure 13.6 The Acrobot as a gymnastic robot.
Referring to Figure 13.4, the cart moves linearly in the x direction subject to an input force F. The pendulum is unactuated, that is, there is no input torque acting at the pivot connecting the pendulum to the cart. Note that the cart-pole system is kinematically identical to a two degree-of-freedom PR robot.
To derive the equations of motion, we let x denote the cart position and θ denote the pendulum angle relative to the vertical position. With the angle convention shown, the (x, y) coordinates of the cart and pendulum mass can be written, respectively, as
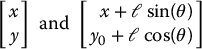
Thus, the cart kinetic energy, Kc, and the pole kinetic energy, Kp, are
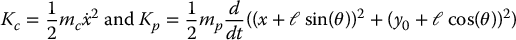
The potential energy of the cart-pole system is
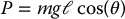
The Euler-Lagrange equations are therefore given by (Problem 13–1)
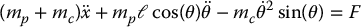
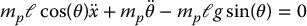
System (13.12)–(13.13) is in the form of an upper-actuated system if we take q1 = x, q2 = θ and u = F.
Note that, if instead we take as generalized coordinates q1 = θ and q2 = x, we can write the system as a lower-actuated system
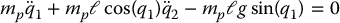
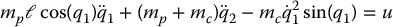
showing that we may use the upper-actuated or lower-actuated models interchangeably as convenient.
13.3.2 The Acrobot
The Acrobot, short for Acrobatic Robot, is a two-link RR robot with actuation at the second link. The Acrobot is representative of a gymnast on a high bar where q2, u2 represent a hip angle and hip torque, respectively. There is no actuator at the first joint where the hands grasp the bar. Referring to Figure 6.9, the dynamic equations of the Acrobot are identical to the two-link RR robot given by Equation (6.90) with the torque at the first joint set to zero.
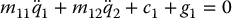
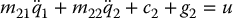
where
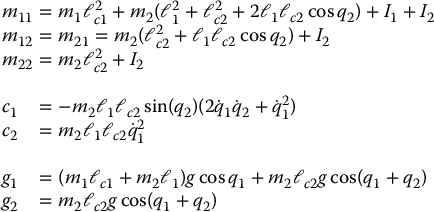
with all parameters defined as in Chapter 6.

Figure 13.7 The Pendubot.
13.3.3 The Pendubot
The Pendubot, or Pendulum Robot, is likewise a two-link RR robot. In this case only the first link is actuated. The Pendubot is a variation of the cart-pole system where the rotational first link plays the role of the cart and is used to balance the passive second link, which plays the role of the pendulum. The dynamic equations are of the form
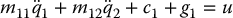
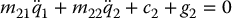
where the left-hand side is identical to the Acrobot dynamics and u is the input torque at the first joint.

Figure 13.8 The Reaction-Wheel Pendulum.
13.3.4 The Reaction-Wheel Pendulum
The Reaction-Wheel Pendulum is a simple pendulum with a rotating disk at the distal end. Actuating the disk results in a reaction torque to move the pendulum.
The dynamic equations of the Reaction-Wheel Pendulum are the simplest of the various examples considered so far. In order to derive the equations of motion for the Reaction-Wheel Pendulum we may observe that if the second link of the Acrobot is counterbalanced to place its center of mass at the axis of the second joint, so that ℓ2 = ℓc2 = 0, then the equations of motion of the Acrobot reduce to those of the Reaction-Wheel Pendulum. Therefore, we leave it as an exercise (Problem 13–2) to show that the equations of motion of the Reaction-Wheel Pendulum can be expressed in the form of a lower-actuated system as
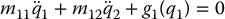
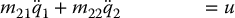
where
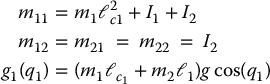
Remark 13.1.
Instead of using the DH convention for the joint angles, if we define the angle of the reaction-wheel relative to the horizontal as shown in Figure 13.9, then it is left as an exercise (Problem 13–3) to show that the equations of motion simplify to
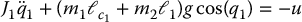

Figure 13.9 The Reaction Wheel Pendulum.
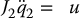
where we define J1 = m1ℓ2c1 + m2ℓ21 and J2 = I2. An additional simplification results if we assume that the mass of the first link is concentrated at joint 2, i.e. ℓc1 = ℓ1 = ℓ. In this case we can write the system as
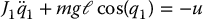
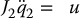
where m = m1 + m2. In this form, the equations of motion of the Reaction-Wheel Pendulum can be seen as the parallel combination of a simple pendulum and a double integrator. Parallel in this context means that Equations (13.24) and (13.25) have the same input u. We will make this more precise in Section 13.7.2 when we discuss passivity-based control.
13.4 Equilibria and Linear Controllability
For a general Lagrangian mechanical system (13.1) with n degrees of freedom we define the state of the system,  , N = 2n, in terms of the generalized coordinates and generalized velocities as
, N = 2n, in terms of the generalized coordinates and generalized velocities as
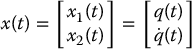
The state equations are then given by
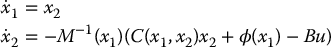
which can be written as
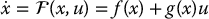
with
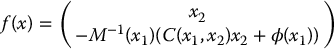
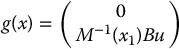
Definition 13.2.
An equilibrium of a dynamical system  is a constant vector (xe, ue) satisfying
is a constant vector (xe, ue) satisfying
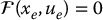
Examining Equations (13.27) and (13.28) we see that x2 = 0 at an equilibrium and therefore the equilibrium configurations are given as solutions of the equation
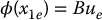
In particular with ue = 0, Equation (13.30) shows that the equilibrium points are local extrema (minima or maxima) of the potential energy, since ϕ is the gradient of the potential energy.
The equilibrium points may be isolated fixed points for each ue as shown below in the case of the Acrobot and Pendubot or they may be non-isolated as happens for systems without potential energy terms. For example, in the absence of potential energy (gravity or elasticity), and with ue = 0, Equation (13.30) shows that every configuration x1 = q in the configuration space  corresponds to an equilibrium point (q, 0) in the state space. The nature of the equilibrium configurations of the system (13.1) is closely related to its controllability properties.
corresponds to an equilibrium point (q, 0) in the state space. The nature of the equilibrium configurations of the system (13.1) is closely related to its controllability properties.
Example 13.2.
Consider the Acrobot/Pendubot with u1 = u2 = 0. It is easy to show (Problem 13–4) that the only equilibrium points belong to the following set:
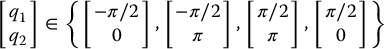
as shown in Figure 13.10.

Figure 13.10 Equilibrium configurations of the Acrobot and Pendubot under gravity with zero input torque.
13.4.1 Linear Controllability
We next discuss the notion of linear controllability, which refers to controllability of the linear approximation of a nonlinear system about an equilibrium.
Definition 13.3.
Given a nonlinear dynamical system
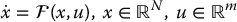
suppose that xe, ue defines an equilibrium of the system, i.e.,  , and let
, and let
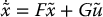
with  ,
,  be the linear approximation of (13.31) at xe, ue. Recall that this means
be the linear approximation of (13.31) at xe, ue. Recall that this means
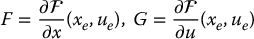
where  and
and  are Jacobian matrices of F(x, u) evaluated at xe, ue. Then the nonlinear system (13.31) is said to be linearly controllable at xe, ue if the linear system (13.32) is a controllable linear system, which is equivalent to the statement that
are Jacobian matrices of F(x, u) evaluated at xe, ue. Then the nonlinear system (13.31) is said to be linearly controllable at xe, ue if the linear system (13.32) is a controllable linear system, which is equivalent to the statement that
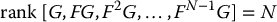
The property of linear controllability allows the design of linear control laws for local exponential stabilization around equilibrium points. In addition, linear controllability is also useful in the context of switching control to achieve global or almost global stability. Systems that are not linearly controllable, such as the nonholonomic systems considered in Chapter 14, require fundamentally different design approaches even for local stabilization as we shall see.
Computation of the Linearization
To compute the linear approximation about an equilibrium of a Lagrangian mechanical system
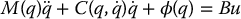
we write the above system in the state space form (13.26) and suppose that xe = (x1e, x2e) and ue define an equilibrium. Note that x1e = qe and  . The Jacobians given by (13.33) are then
. The Jacobians given by (13.33) are then
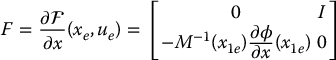
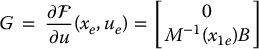
To see why this is true, note that the Coriolis and centrifugal terms  are quadratic in the velocities and hence their partial derivatives vanish at
are quadratic in the velocities and hence their partial derivatives vanish at  . Likewise, the partial derivative of M− 1 is multiplied by ϕ − Bu, which also vanishes at the equilibrium. The details are left as an exercise (Problem 13–5).
. Likewise, the partial derivative of M− 1 is multiplied by ϕ − Bu, which also vanishes at the equilibrium. The details are left as an exercise (Problem 13–5).
A Necessary Condition for Linear Controllability
We can therefore write the linear approximation of the system in state space using (13.35) and (13.36) as
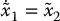
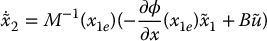
Since M(qe) has full rank n, it follows that  must have full row rank in order for the linearization to be controllable. For a lower-actuated system, i.e.
must have full row rank in order for the linearization to be controllable. For a lower-actuated system, i.e.  , we can express Equations (13.37) and (13.38) as
, we can express Equations (13.37) and (13.38) as
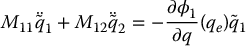
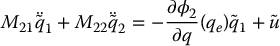
It follows that  must have full row rank. Since
must have full row rank. Since  has dimension ℓ × m, it is necessary that m ⩾ ℓ. Therefore, we can state the following
has dimension ℓ × m, it is necessary that m ⩾ ℓ. Therefore, we can state the following
Proposition 13.1
A lower-actuated system is linearly controllable at an equilibrium q = qe,  , u = ue only if
, u = ue only if
- m ⩾ ℓ, that is, the number of active joints is at least as great as the number of passive joints, and
 has full row rank.
has full row rank.
Remark 13.2.
An identical argument shows that an upper-actuated system is linearly controllable only if
- m ⩾ ℓ, that is, the number of active joints is at least as great as the number of passive joints, and
 has full row rank.
has full row rank.
An important implication of Proposition 13.25 is that each passive joint axis must have a non-zero potential force, such as a gravitational or an elastic force, at a given equilibrium configuration in order to be linearly controllable at that equilibrium. In particular, serial-link robots without gravitational or elastic forces at the passive joints are never linearly controllable.
Example 13.3.
Consider the Reaction-Wheel Pendulum
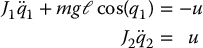
which is equivalent to the lower-actuated system
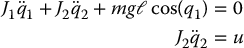
It follows immediately from Proposition 13.1 that the system is linearly controllable only if mgℓ is nonzero. In this case, the condition turns out to be sufficient as well. With state vector  we can write this system in state space as
we can write this system in state space as
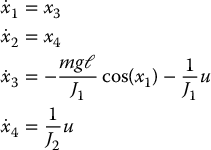
It is easily computed that xe = ( ± π/2, 0, 0, 0) are equilibrium points and that the linear approximations about these equilibrium points are
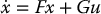
where
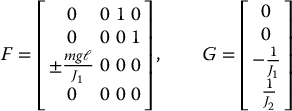
It is left as an exercise (Problem 13–6) to show that the linearized systems at each equilibrium are controllable if and only if  is nonzero.
is nonzero.
Example 13.4.
Let’s consider the problem of designing a control law to balance the Reaction-Wheel Pendulum about the inverted equilibrium q1 = π/2, q2 = 0 (with zero velocity). For simplicity we take m = ℓ = J1 = J2 = 1. Therefore, with g = 9.8, the linear approximation at the inverted equilibrium is
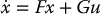
with
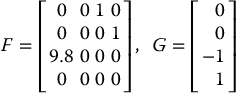
A stabilizing controller u = −kTx for this linear system can be found using Matlab’s lqr function that computes the optimal control minimizing
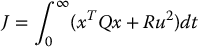
subject to (13.41). With Q as the 4 × 4 identity matrix and r = 1, the optimal gain turns out to be
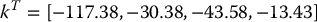
A particular response of the system with this controller is shown in Figure 13.11.
Example 13.5.
We next give a more detailed example using the Pendubot that gives further insight into the property of linear controllability. Figure 13.10 showed the equilibrium configurations of the Pendubot with zero input torque. A nonzero constant torque ue can hold the first link at a fixed value q1e. Specifically, with the gravitational torque at link 1 given by Equation (5.85)
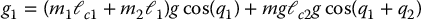
let q1e be any desired angle and take q2e so that q1e + q2e = π/2 or 3π/2. Then since cos (q1e + q2e) = ±1 the constant torque input
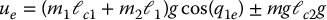
corresponds to equilibrium configurations of the type shown in Figure 13.12. The Pendubot thus has a rich set of configurations to balance the second link.
Since the gravitational torque at the second link is given by
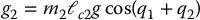
it follows from Proposition 13.1 that the system is linearly controllable only if sin (q1e + q2e) ≠ 0, which is satisfied at each equilibrium configuration q1e + q2e = ±π/2. In fact, the Pendubot is linearly controllable at each such equilibrium except when the first link is horizontal, as we show next.
Since the Pendubot is upper-actuated, a straightforward calculation shows that the linear approximation at any equilibrium xe is
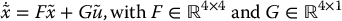
where
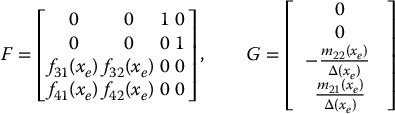
with
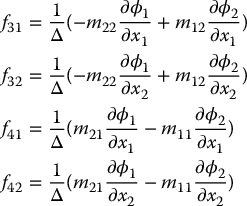
and Δ = m11m22 − m12m21.
Using the parameters in Table 13.1 we can compute the linear approximation for each q1e ∈ [0, π/2] with q2e = π/2 − q1e, and we denote by  the 4 × 4 controllability matrix,
the 4 × 4 controllability matrix,  .
.
Figure 13.13 shows a plot of the determinant of the controllability matrix  in the interval q1e ∈ [0, π/2] showing that the linear system is uncontrollable at q1e = 0 and controllable at all other equilibria in this interval.
in the interval q1e ∈ [0, π/2] showing that the linear system is uncontrollable at q1e = 0 and controllable at all other equilibria in this interval.

Figure 13.11 Local stabilization of the Reaction-Wheel Pendulum at the inverted position q1 = π/2, q2 = 0.

Figure 13.12 Equilibrium configurations of the Pendubot for ue nonzero.
Table 13.1 Example Pendubot inertia parameters.
| m1 | m2 | ℓ1 | ℓc1 | ℓc2 | I1 | I2 |
| 1 | 1 | 2 | 1 | 1 | 1 | 1 |

Figure 13.13 The determinant of the controllability matrix for equilibrium positions (0, π/2) to (π/2, 0). The Pendubot is not linearly controllable at q1e = 0, q2e = π/2, but is linearly controllable at all other equilibria.
13.5 Partial Feedback Linearization
In this section we introduce the notions of collocated and noncollocated partial feedback linearization for underactuated robots. By collocated partial feedback linearization we mean using nonlinear feedback to create a linear relationship between the accelerations of the active joints and their respective inputs. Noncollocated partial feedback linearization means establishing a linear relationship between the accelerations of the passive joints and the inputs to the active joints. In both cases, we obtain systems of double integrator equations, of the form
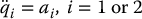
where ai is an outer-loop control, as in the case of the inverse dynamics in Chapter 9. Both the collocated and noncollocated partial feedback linearization approaches lead to normal forms that are useful to design control laws in a host of applications, including the control of gymnastic robots, bipedal walking robots, snake robots, and others.
13.5.1 Collocated Partial Feedback Linearization
Consider the lower-actuated system1
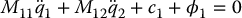
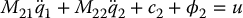
Let us examine in more detail the first equation (13.42) above
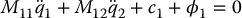
The term  is nonsingular as a result of the uniform positive definiteness of the robot inertia matrix M. Therefore, we may solve for
is nonsingular as a result of the uniform positive definiteness of the robot inertia matrix M. Therefore, we may solve for  in (13.44) as
in (13.44) as
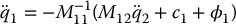
and substitute the resulting expression (13.45) into (13.43) to obtain
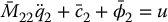
where the terms  ,
,  and
and  are given by (Problem 13–7)
are given by (Problem 13–7)
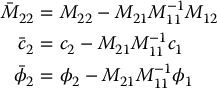
Proposition 13.2
The m × m matrix  is symmetric and positive definite at each
is symmetric and positive definite at each  .
.
Proof: To see this, it is left as an exercise (Problem 13–8) to show that
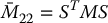
where S is the n × m matrix
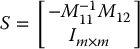
with Im × m denoting the m × m identity matrix. Since the matrix S has rank m for all q and M is symmetric, positive definite, it follows that  is likewise symmetric and positive definite.
is likewise symmetric and positive definite.
Referring to Appendix B, we see that the matrix  is the Schur complement of M22 in M. Now, by inspection, we can see that the control law
is the Schur complement of M22 in M. Now, by inspection, we can see that the control law
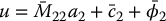
where  is an additional outer-loop control term, results in
is an additional outer-loop control term, results in
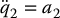
The complete system up to this point may be written as
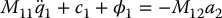
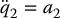
Definition 13.4.
The system (13.52)–(13.53) is called a second-order normal form with input-driven internal dynamics, or simply second-order normal form. Equation (13.52) is called the internal dynamics.
Since the system (13.52)–(13.53) is feedback equivalent to the original system it can be used as a starting point for subsequent control analysis and design.
Example 13.6.
Consider the cart-pole system given by Equations (13.14)–(13.15) and let us normalize all constants to unity for simplicity
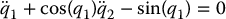
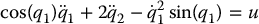
It is easy to show (Problem 13–10) that the collocated partial feedback linearization control
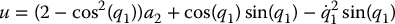
results in the normal form
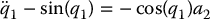
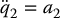
13.5.2 Noncollocated Partial Feedback Linearization
In the previous section we showed that the dynamics of the active degrees of freedom can be globally linearized by nonlinear feedback. In this section we show, under a condition regarding the degree of coupling among the active and passive degrees of freedom, that a similar partial feedback linearizing control can linearize the dynamics of the passive degrees of freedom. This is an interesting and, at first glance, somewhat surprising result. In this case, the linearization may hold either locally or globally.
Consider again the lower-actuated system
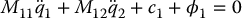
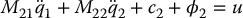
The inertia matrix terms M12 and M21 = MT12 generate coupling generalized forces among the degrees of freedom. For example, a control input torque u in (13.60) will not only result in an acceleration of the active degrees of freedom q2 but also an acceleration of the passive degrees of freedom q1, and the latter acceleration will depend on these off-diagonal terms in the inertia matrix M(q). Since M12 is an ℓ × m matrix, we make the following definition:
Definition 13.5.
Let  be an open subset of the configuration space
be an open subset of the configuration space  . The system (13.59)–(13.60) is said to be strongly inertially coupled in
. The system (13.59)–(13.60) is said to be strongly inertially coupled in  if and only if
if and only if
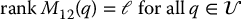
Note that since M12 is an ℓ × m matrix and there are m control inputs, the condition of strong inertial coupling requires that m ⩾ ℓ, i.e. that the number of active degrees of freedom be at least as great as the number of passive degrees of freedom.
If M12 has full rank ℓ, it follows that the ℓ × ℓ matrix M12MT12 has rank ℓ and is therefore invertible. Thus, under the assumption of strong inertial coupling, we let
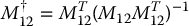
be the right pseudoinverse of M12 as defined in Appendix B. We may therefore write  in Equation (13.59) as
in Equation (13.59) as
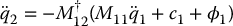
and substitute this expression for  into Equation (13.60) to obtain
into Equation (13.60) to obtain
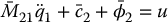
where
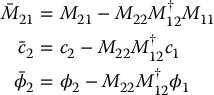
A calculation similar to that previously given for  shows that
shows that  has full rank ℓ since
has full rank ℓ since
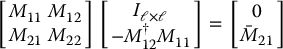
Thus, with the control input
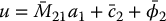
we obtain
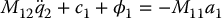
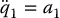
The system (13.66)–(13.67) is also in second-order normal form and Equation (13.66) represents the input-driven internal dynamics.
Example 13.7.
The cart-pole system (13.54)–(13.55) satisfies the strong inertial coupling condition in the interval  . It can therefore be shown (Problem 13–11) that the noncollocated control law
. It can therefore be shown (Problem 13–11) that the noncollocated control law
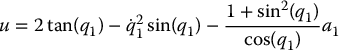
results in the feedback equivalent system
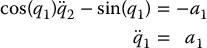
which is valid in the interval  .
.
Example 13.8.
Consider next the Reaction-Wheel Pendulum in the collocated second-order normal form
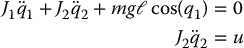
Since J2 ≠ 0 is constant, the strong inertial coupling condition is satisfied globally. It is easy to see that the control input
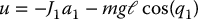
results in the noncollocated second-order normal form
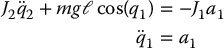
13.6 Output Feedback Linearization
In this section we introduce the notions of output feedback linearization, relative degree, and zero dynamics for underactuated mechanical systems. The goal of output feedback linearization is to create a linear input/output relationship using feedback control and is related to both the partial feedback linearization considered in Section 13.5 and the state feedback linearization problem considered in Chapter 12. In fact, the partial feedback linearization in Section 13.5 is a special case of output feedback linearization as we shall see.
We also introduce the notion of virtual holonomic constraints. Virtual holonomic constraints (VHCs) are constraints that are maintained by feedback control, using the active degrees of freedom, rather than being imposed by the natural dynamics of the robot or the environment and are useful to generate coordinated motion among the active and passive joints. VHCs are particularly useful in locomotion, for example for control of walking robots, snake robots, brachiation robots, and gymnastic robots.
Consider again a lower-actuated system in second-order normal form and suppose that we have a p-dimensional output  defined as a smooth function of the configuration q = (q1, q2)
defined as a smooth function of the configuration q = (q1, q2)
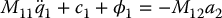
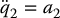
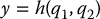
Differentiating the output y yields
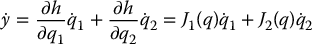
where  . Computing the second derivative
. Computing the second derivative  of y, and substituting for
of y, and substituting for  and
and  from (13.68) and (13.69) yields
from (13.68) and (13.69) yields
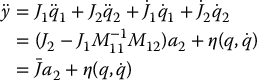
where  is a p × m matrix, called the decoupling matrix and
is a p × m matrix, called the decoupling matrix and  .
.
The system (13.68)–(13.70) is said to have vector relative degree two provided the decoupling matrix  has full rank. The relative degree can be interpreted as the number of times the output y(t) must be differentiated before the input a2 appears. Since
has full rank. The relative degree can be interpreted as the number of times the output y(t) must be differentiated before the input a2 appears. Since  is a p × m matrix, the relative degree is well defined provided the rank of
is a p × m matrix, the relative degree is well defined provided the rank of  is equal to p at each configuration q. Note that the relative degree can be well-defined globally or locally for q in a subset of the configuration space. Note also that for the relative degree to be well defined it is necessary that m ⩾ p, i.e., that the number of outputs does not exceed the number of active degrees of freedom.
is equal to p at each configuration q. Note that the relative degree can be well-defined globally or locally for q in a subset of the configuration space. Note also that for the relative degree to be well defined it is necessary that m ⩾ p, i.e., that the number of outputs does not exceed the number of active degrees of freedom.
Under the assumption that  has full rank, we can then define the control input a2, using the right pseudo-inverse
has full rank, we can then define the control input a2, using the right pseudo-inverse  of
of  , as
, as
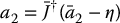
to obtain the linearized and decoupled output equation
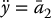
and we note that an outer-loop control  can easily be designed to stabilize the equilibrium y = 0 or to track an arbitrary reference trajectory yd(t) in (13.73).
can easily be designed to stabilize the equilibrium y = 0 or to track an arbitrary reference trajectory yd(t) in (13.73).
Definition 13.6.
With output y = h(q1, q2), let  . Γ is called the zero-dynamics manifold. An outer-loop control a2 that asymptotically stabilizes the equilibrium y = 0 in (13.73) makes Γ an invariant manifold for the system (13.68)–(13.70). In this case, Γ is called a controlled-invariant manifold. The reduced-order dynamics on Γ are called the zero dynamics.
. Γ is called the zero-dynamics manifold. An outer-loop control a2 that asymptotically stabilizes the equilibrium y = 0 in (13.73) makes Γ an invariant manifold for the system (13.68)–(13.70). In this case, Γ is called a controlled-invariant manifold. The reduced-order dynamics on Γ are called the zero dynamics.
Remark 13.3.
Returning to the general lower-actuated system
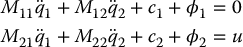
it is straightforward to show (Problem 13–12) that if we take as output y = q2, then the control input given by Equation (13.50) achieves both output linearization and places the system in the collocated second-order normal form.
Likewise, the noncollocated second-order normal form is achieved via output feedback linearization with the choice of output y = q1 (Problem 13–13).
13.6.1 Computation of the Zero Dynamics
For a general output function h(q1, q2), it is not easy to characterize the reduced-order dynamics on the zero-dynamics manifold Γ. In the special cases y = qi, i = 1 or 2, the zero dynamics can be easily characterized and has a nice physical interpretation as we show in this section.
Let’s first take as output y = q2. Therefore, p = m and the decoupling matrix is just Im × m, the m × m identity matrix. With this output, we have
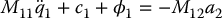
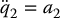
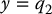
The zero dynamics are found by setting the output y identically zero, which implies that q2 = 0,  , and a2 = 0 in Equation (13.74). Setting
, and a2 = 0 in Equation (13.74). Setting
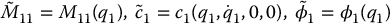
the zero dynamics are given by the system
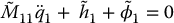
The reduced-order model (13.78) represents the dynamics of a robot with ℓ passive joints where the m active joints are fixed, at q2 = 0, and is therefore a (reduced-order) Lagrangian mechanical system.
Let E be the total energy of the reduced-order system (13.78).
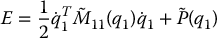
Then, from the standard properties of Lagrangian dynamics, we know that  along trajectories of the system (13.78). The implication is that trajectories of the zero dynamics are constant energy levels of the reduced-order system.
along trajectories of the system (13.78). The implication is that trajectories of the zero dynamics are constant energy levels of the reduced-order system.
Example 13.9.
Consider the Acrobot model in second-order normal form
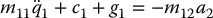
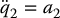
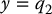
The zero dynamics are found by setting q2 = 0,  , and a2 = 0 in (13.80). From Equation (5.83) we have
, and a2 = 0 in (13.80). From Equation (5.83) we have
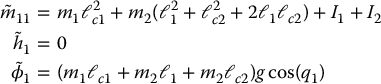
Substituting these expressions into (13.80) we end up with
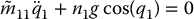
where
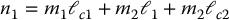
Note that these zero dynamics are just the dynamics of a simple pendulum.
Since almost all trajectories on the above zero dynamics manifold are periodic orbits the equilibrium solutions are not asymptotically stable. Such systems are called nonminimum phase systems.
In the case of noncollocated partial feedback linearization, consider again the normal form equations
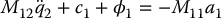
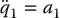
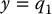
with output y = q1. Note that the strong inertial coupling condition that is necessary for the existence of the above normal form ensures that the number of outputs is less than the number of active joints. In this case, the zero dynamics are found by setting q1 = 0,  , and a1 = 0 in the above system, which leads to
, and a1 = 0 in the above system, which leads to
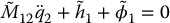
with  ,
,  ,
,  . Equation (13.86) need not, in general, represent a Lagrangian system since the ℓ × m matrix M12 is not guaranteed to be symmetric or positive definite, even in the case ℓ = m.
. Equation (13.86) need not, in general, represent a Lagrangian system since the ℓ × m matrix M12 is not guaranteed to be symmetric or positive definite, even in the case ℓ = m.
Feedback Linearization of the Reaction-Wheel Pendulum
As we noted in the introduction to this chapter, underactuated robots are generally not fully feedback linearizable. The best one can achieve in most cases is partial feedback linearization, either collocated or noncollocated. It is interesting, therefore, that the Reaction-Wheel Pendulum is an example of a robot that is fully feedback linearizable. In order to see this, let’s return to the model for the Reaction-Wheel Pendulum
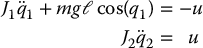
and choose the output equation
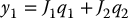
Then computing successive derivatives of y1 we get
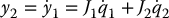
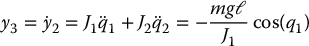
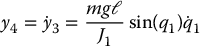
Then  satisfies
satisfies
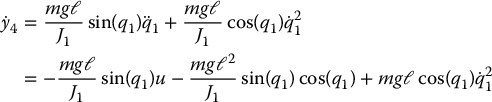
Therefore, the control input
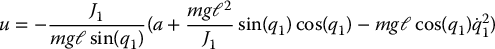
results in the linear system in Brunovsky canonical form
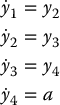
with output y = y1. We note therefore that the output (13.87) has relative degree four in the region 0 < q1 < π and the control input (13.91) is valid in this same region. Thus the Reaction-Wheel Pendulum is locally output feedback linearizable. As a result the inverted equilibrium can be stabilized with the above feedback linearizable control law provided that the initial orientation of the pendulum is above the horizontal position where 0 < q1 < π. However, one must be careful that the transient response does not violate this constraint, which may happen if there is a large initial velocity or if the control results in undershoot. Problem 13–14 deals with the design of the outer-loop control term a in (13.91).
13.6.2 Virtual Holonomic Constraints
We next introduce the notion of virtual holonomic constraints for underactuated robots and discuss the relation to output feedback linearization.
Definition 13.7.
Let  be a smooth function of the configuration variables with rank(dhq) = p for all q ∈ h− 1(0). The function h is said to define a virtual holonomic constraint for a given underactuated system if there exists a feedback control such that
be a smooth function of the configuration variables with rank(dhq) = p for all q ∈ h− 1(0). The function h is said to define a virtual holonomic constraint for a given underactuated system if there exists a feedback control such that
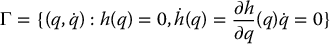
is a controlled-invariant manifold for the system.
The term virtual constraint arises from the fact that, if the system is initialized on Γ, i.e, h(q(0)) = 0, then the solution trajectory q(t) remains on Γ for all t > 0. We can immediately see that a useful way to enforce a given set of virtual holonomic constraints is to define an output function y = h(q1, q2) and design the control u to achieve output feedback linearization. This will work provided the constraint function h yields an output function with vector relative degree two.
Example 13.10.
Suppose that we wish to constrain the motion of the Acrobot such that q1(t) + 0.5q2(t) = 0. This motion simulates a so-called continuous contact brachiation. Figure 13.14 shows the response with the output y = h(q1, q2) = q1 + 0.5q2 as a virtual holonomic constraint and an output-linearizing control.

Figure 13.14 Brachiation motion of the Acrobot with virtual holonomic constraint q1 + 0.5q2 = 0.
13.7 Passivity-Based Control
In this section we discuss the use of Energy and Passivity methods for control of underactuated robots. We recall from Chapter 6 that the total energy E for a Lagrangian mechanical system
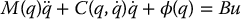
satisfies
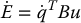
which means that the system defines a passive map from input Bu to output  . Thus energy and passivity are intimately related for the class of mechanical systems that we consider. In Chapter 6 we used the passivity property to derive robust and adaptive control laws for fully-actuated n-link manipulators. We will show in this section that passivity, combined with switching control and saturation, provides elegant solutions for control of underactuated robots. Specifically, we will focus on the problem of swingup and balance; for example, in the case of the Acrobot, swingup and balance mimics the motion of a gymnast performing a handstand on a high bar.
. Thus energy and passivity are intimately related for the class of mechanical systems that we consider. In Chapter 6 we used the passivity property to derive robust and adaptive control laws for fully-actuated n-link manipulators. We will show in this section that passivity, combined with switching control and saturation, provides elegant solutions for control of underactuated robots. Specifically, we will focus on the problem of swingup and balance; for example, in the case of the Acrobot, swingup and balance mimics the motion of a gymnast performing a handstand on a high bar.
As we shall see, the problem of swingup and balance is readily accomplished using energy/passivity methods combined with switching control. The balance control problem is essentially the problem of stabilizing the equilibrium at the inverted configuration and is solvable locally with linear feedback control as we have previously illustrated. The swingup control problem then becomes one of controlling the state of the system so that the trajectory enters the region of attraction of the balance controller, at which point control can be switched to the balance control.
13.7.1 The Simple Pendulum
To motivate the subsequent treatment, consider a simple pendulum of length ℓ and mass m as shown in Figure 13.15. Assume that a force F acts on the end of the pendulum as shown. We can think of this pendulum as a simplified model of a passive link in a larger system where the force F arises from the motion of active links, for example, by actively swinging the second link in the case of the Acrobot. Note that the force F induces a torque τ = ℓF at the pendulum pivot. The equation of motion of this system is therefore given by

Figure 13.15 A simple pendulum with a force F acting at the bob.
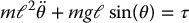
and the total energy is
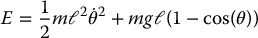
With τ equal to zero, the pendulum energy is constant along solution trajectories of (13.94). Stated another way, the set
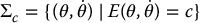
defines a trajectory of the system in the sense that, if  , the solution of (13.94) with F = 0 satisfies
, the solution of (13.94) with F = 0 satisfies  for t > 0. The set Σc is an invariant manifold called a first integral of motion for the simple pendulum.
for t > 0. The set Σc is an invariant manifold called a first integral of motion for the simple pendulum.
Figure (13.16) shows a portion of the phase portrait of the unforced pendulum where each trajectory corresponds to a particular energy level. Each trajectory of the simple pendulum is periodic with the exception of the equilibrium configurations (0, 0) and ( ± π, 0), and the so-called homoclinic orbit. We have seen previously that the simple pendulum is relevant for more complicated underactuated systems, for example, appearing as the zero dynamics manifold in Example 13.25.

Figure 13.16 Phase portrait of the simple pendulum. The constant energy curves are solution trajectories. Figure generated by pplane, courtesy of John C. Polking, Rice University.
Definition 13.8.
A homoclinic orbit of a dynamical system is a trajectory that connects a saddle-point equilibrium to itself. A homoclinic orbit lies in the intersection of the stable and unstable manifolds of the saddle point.
With regard to the phase portrait of the simple pendulum in Figure 13.16, the trajectory that connects the saddle-point equilibria ( − π, 0) and ( + π, 0) is a homoclinic orbit if we identify ( − π, 0) and ( + π, 0).
Let us now consider the problem of using the force F as a feedback control law to control the energy of the pendulum. In other words, given a constant c > 0, we wish to design the input τ = ℓF so that the energy E(t) converges to c. In doing so, the motion of the pendulum will converge to the particular periodic solution defined by E = c. With this in mind let V be a Lyapunov function candidate defined as
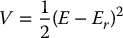
where Er = c is chosen as a reference energy. Then  is given by
is given by
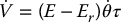
Note that the above expression means that the system is passive from input τ to output  . If we take the input τ as
. If we take the input τ as
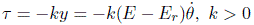
we end up with
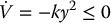
An elementary application of LaSalle’s theorem (Problem 13–15) shows that all trajectories converge either to a trajectory with energy Er = c or to  .
.
Remark 13.4.
The condition,  , cannot be ruled out since the open-loop equilibrium solutions (0, 0) and ( ± π, 0), remain equilibrium points for the closed-loop system since the control input is zero if
, cannot be ruled out since the open-loop equilibrium solutions (0, 0) and ( ± π, 0), remain equilibrium points for the closed-loop system since the control input is zero if  . However, the equilibrium (0, 0) is now unstable for the closed-loop system (Problem 13–16).
. However, the equilibrium (0, 0) is now unstable for the closed-loop system (Problem 13–16).
With Ec as the energy on the homoclinic orbit, Figure 13.17 shows the phase portrait of the closed loop system.

Figure 13.17 Phase portrait of the closed-loop system. Figure generated by pplane, courtesy of John C. Polking, Rice University.

Figure 13.18 The Reaction-Wheel Pendulum as a parallel interconnection of passive systems.
Saturation
An important property of the passivity-based control approach is that bounds on the available control effort (i.e., saturation) are easily handled. To see this, suppose that the above input τ constrained as |τ| ⩽ m. We can choose the control input as
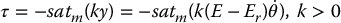
where satm( · ) is the saturation function
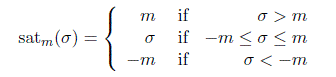
The saturation function is a so-called first and third quadrant nonlinearity which means that
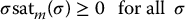
Therefore, using the control (13.100) in place of (13.98) we have
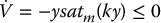
We leave it as an exercise (Problem 13–17) to show that the conclusions from the application of LaSalle’s theorem remain the same with the above saturation control.
13.7.2 The Reaction-Wheel Pendulum
In this section we consider the swingup control problem for the Reaction-Wheel Pendulum using the tools derived above. Consider again the Reaction-Wheel Pendulum dynamics in the form
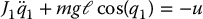
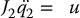
Here we see that the Reaction-Wheel Pendulum dynamics are described by a parallel connection of a simple pendulum and a double integrator
both of which satisfy a passivity property from input torque to output velocity. Specifically, with
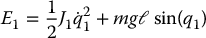
the usual energy of the pendulum and
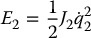
the energy of the reaction wheel, we have
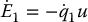
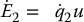
Since the parallel interconnection of passive systems is passive (Problem 13–18), it remains to define a suitable output y for the parallel interconnection. Following the previous example of the simple pendulum, we can define a Lyapunov function V as
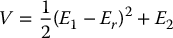
where Er is a constant reference energy for the pendulum. A straightforward calculation then gives
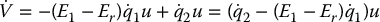
Thus if we define  as a new output we get
as a new output we get
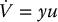
and therefore the system is passive from input u to output y. We can then choose the control input u as
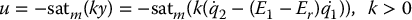
Proposition 13.3
Let Er > 0 be a constant reference value for the Reaction-Wheel Pendulum energy E1. Choose the control input u in (13.101)–(13.102) according to (13.108). Then all trajectories of the closed-loop system converge to the set
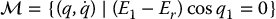
Proof: The proof is a straightforward calculation using LaSalle’s theorem and is left as an exercise (Problem 13.–19).
Therefore, all trajectories of the closed loop system will converge either to E1 = Er or to cos (q1) = 0. In the first case, that E1 = Er, it follows from (13.108) that the velocity of the reaction wheel  . In the second case, that cos (q1) = 0, it follows that q1 = nπ and
. In the second case, that cos (q1) = 0, it follows that q1 = nπ and  .
.
Figures 13.19 and 13.20 show the simulation with Er equal to the energy of the homoclinic orbit of the pendulum with a switch to a linear balancing controller at t = 8 seconds.

Figure 13.19 Swingup and balance of the Reaction-Wheel Pendulum (left) and phase plane trajectory of the pendulum (right).

Figure 13.20 Reaction-wheel velocity (left) and saturated control input (right).
13.7.3 Swingup and Balance of The Acrobot
We next consider the swingup and balance for the Acrobot, beginning in the collocated second-order normal form in Example (13.9).
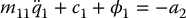
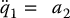
It is important that the internal dynamics in the second-order normal form is driven by the outer-loop control term a2 so that we can use this term both to stabilize the linearized subsystem of the system and modify the internal dynamics.
The inverted equilibrium for the Acrobot model is q1 = +π/2,  , q2 = 0,
, q2 = 0,  . Suppose that we define the outer-loop control a2
. Suppose that we define the outer-loop control a2
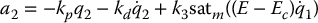
where E is the total energy of the Acrobot and Ec is the energy at the inverted equilibrium. A successful swingup and balance motion with this strategy is shown in Figure 13.21, where control is switched to an LQR balance control at approximately 7.5 seconds.

Figure 13.21 Swingup and balance of the Acrobot using switching control
13.8 Chapter Summary
In this chapter we discussed the control of underactuated mechanical systems with a focus on underactuated serial-link mechanisms. Many of the control techniques for fully-actuated systems that we discussed in previous chapters do not apply without modification to the class of underactuated systems. One of the primary obstructions to control of this class of systems is the presence of non-minimum phase zero dynamics.
Upper and Lower-Actuated Models
The class of robots that we treated in this chapter is characterized as n-degree-of-freedom Lagrangian dynamical systems with m < n control inputs, and thus, m actuated degrees of freedom and ℓ = n − m unactuated degrees of freedom. The difference ℓ = n − m is the degree of underactuation of the system. We showed that any such system may be represented either as an upper-actuated system
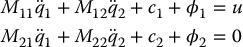
with  and
and  , or as a lower-actuated system
, or as a lower-actuated system
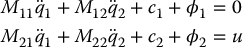
with  and
and  .
.
Linear Controllability
Classifying underactuated systems by whether or not they are linearly controllable is useful for determining the global controllability properties. We showed that a necessary condition for linear controllability is that each passive degree of freedom must have a nonzero potential force such as elasticity or gravitational force. The property of linear controllability allows one to apply switching control methods that combine nonlinear control laws far from the equilibrium and linear control laws close to the equilibrium. We illustrated this idea for problems of swingup and balance of the Acrobot and the Reaction-Wheel Pendulum.
Collocated and Noncollated Partial Feedback Linearization
We introduced the notions of collocated and noncollocated partial feedback linearization, which transforms a given underactuated system into a second-order normal form that is important for subsequent analysis and controller design. The second-order normal form in the collocated case is
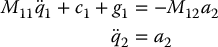
The second-order normal form in the noncollocated case is
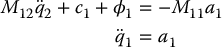
where a2, respectively a1, are additional (outer-loop) controls.
Output Feedback Linearization and Virtual Holonomic Constraints
A virtual holonomic constraint is a relation of the form h(q) = 0, where  is a smooth function from the configuration space
is a smooth function from the configuration space  to
to  that is enforced by the feedback control. Virtual constraints may be chosen as an output function to achieve a desired task, such as coordinated motion among the degrees of freedom. Enforcing the virtual constraints leads to the notion of zero dynamics, which are the dynamics of the system restricted to a reduced-order manifold in the state space of the full system.
that is enforced by the feedback control. Virtual constraints may be chosen as an output function to achieve a desired task, such as coordinated motion among the degrees of freedom. Enforcing the virtual constraints leads to the notion of zero dynamics, which are the dynamics of the system restricted to a reduced-order manifold in the state space of the full system.
Switching Control and Passivity
Starting with the second-order normal form we showed how stabilization to fixed points can be accomplished by energy-based methods and switching control. Energy shaping methods have the advantage of not relying on the need to plan time-based trajectories for tracking.
Problems
- Complete the derivation of the Euler–Lagrange equations (13.12)–(13.13) for the cart-pole system from the expressions for the kinetic and potential energy given in (13.10)–(13.11).
- Show that the dynamic equations of the Acrobot reduce to those of the Reaction Wheel Pendulum if ℓc2 = 0.
- Verify the claims of Remark 13.25 by deriving Equations (13.22)–(13.23) and (13.24)–(13.25).
- Show that, with ue = 0, the only equilibrium points of the Acrobot and Pendubot are shown in Figure 13.10.
- Verify the expressions for the matrices F and G in Equations (13.35)–(13.36).
- Show by direct calculation that the linearized equations of motion of the Reaction-Wheel Pendulum about the origin are controllable if and only if the constant term
 is nonzero.
is nonzero. - Verify the expressions for the terms
 ,
,  and
and  in Equations (13.47).
in Equations (13.47). - Complete the proof of Proposition 13.2.
- Verify the expression for the control law (13.65).
- Complete the calculations to verify the collocated control law for the cart-pole system in Example 13.4.
- Complete the calculations to verify the noncollocated control law for the cart-pole system in Example 13.4.
- Consider the lower-actuated system
Show that if we take as an output y = q2 for this system, where qr2 is a constant reference vector for q2, then the control input u that achieves the linear system (13.73) is identical to the control u given by Equation (13.50) and therefore achieves both output linearization and places the system in normal form.
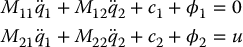
- Show for the system of Problem 12 that the noncollocated second-order normal form is achieved via output feedback linearization with the choice of output y = q1.
- Design a linear outer-loop control a in equation (13.91) to stabilize the Reaction-Wheel Pendulum at the inverted position. Investigate the response for various initial conditions.
- Using the expression for
 in Equation (13.99), show that all trajectories of the simple pendulum converge to those with energy Er or to ω = 0.
in Equation (13.99), show that all trajectories of the simple pendulum converge to those with energy Er or to ω = 0. - Consider the simple pendulum with control law (13.98). Show that the equilibrium (0, 0) is unstable for Er = 2 and stable (but not asymptotically stable) for 0 ⩽ Er < 2.
- Use LaSalle’s theorem to show that applying the control (13.100) in place of (13.98) for swingup of the simple pendulum yields the same asymptotic behavior.
- Show that the parallel interconnection of passive systems is passive.
- Complete the proof of Proposition 13.3 using LaSalle’s theorem.
- Using the cart-pole system, derive and simulate a swingup and balance control using any of the methods in this chapter.
Notes and References
Research in the control of underactuated mechanical systems is an active area and there is a large body of literature devoted to the subject. Research monographs specifically for control of underactuated systems are [186, 41, 179]. Proposition 13.1 is taken from [98]. Most of the material on collocated and noncollocated partial feedback linearization presented here is taken from [162]. Related work followed in [157, 159, 163]. The second-order normal forms for both the collocated and noncollocated case is attributed to [162]. Several treatments of second-order nonholonomic constraints are found in [130, 183, 123, 151]. The classical inverted pendulum has been studied extensively in the control literature [127, 62, 117, 184]. The Acrobot first appeared in [122], where it was shown that the Acrobot dynamics are not feedback linearizable. The swingup problem for the Acrobot was first solved in [158]. The Pendubot [160] and the Reaction-Wheel Pendulum [164] both came out of the University of Illinois College of Engineering Control Systems Laboratory. A rather complete monograph devoted entirely to the Reaction-Wheel Pendulum is [14], which includes the passivity-based control approach presented here. The concept of virtual constraints and it’s application to bipedal locomotion is due to [59].
Note
- 1 As noted before, we could just as easily choose to work with the upper-actuated system.