CHAPTER 11
VISION-BASED CONTROL
In Chapter 10 we described methods to control the forces and torques applied by a manipulator interacting with its environment. Force feedback is most useful when the end effector is in physical contact with the environment. During free motion, such as moving a gripper toward a grasping configuration, force feedback provides no information that can be used to guide the motion of the gripper. In such situations, noncontact sensing, such as computer vision, can be used to control the motion of the end effector relative to environment.
In this chapter we consider the problem of vision-based control. Unlike force control, with vision-based control the quantities of concern are typically not measured directly by the sensor. For example, if the task is to grasp an object, the quantities of concern are pose variables that describe the position of the object and the configuration of the gripper. A vision sensor provides a two-dimensional image of the workspace, but does not explicitly contain any information regarding the pose of the objects in the scene. There is, of course, a relationship between this image and the geometry of the robot’s workspace, but the task of inferring the 3D structure of the scene from an image is a difficult one, and a full solution to this problem is not required for most robotic manipulation tasks. The problem faced in vision-based control is that of extracting a relevant set of parameters from an image and using these parameters to control the motion of the manipulator in real time to perform the desired task.
Over the years several approaches have been developed for vision-based control. These vary based on how the image data are used, the relative configuration of camera and manipulator, choices of coordinate systems, etc. We begin this chapter with a discussion of these issues. Following this discussion, we provide a brief introduction to computer vision. We focus on those aspects of computer vision that are directly relevant to vision-based control, namely imaging geometry and features that can be extracted directly from image data. We then develop the differential kinematics that relate camera motion to changes in these features, deriving the so-called interaction matrix. We use the interaction matrix to develop image-based control laws, motivated by Lyapunov theory. When introducing these concepts, we focus primarily on image-based visual servo control for eye-in-hand camera systems. In such systems, the problem is to control the motion of a hand-held camera based on information that can be directly extracted from an image, without resorting to computing a representation of the 3D scene geometry. After developing the main theory for image-based eye-in-hand systems, the remainder of the chapter considers a number of other issues related to vision-based control, including generalization of camera-manipulator configuration, alternative control schemes, and criteria for optimality in control design.
11.1 Design Considerations
A number of questions confront the designer of a vision-based control system. What kind of camera should be used? Should a zoom lens or a lens with fixed focal length be used? How many cameras should be used? Where should the cameras be placed? What image information should be used to control the motion? Should the vision system be used to infer a three-dimensional description of the scene, or should two-dimensional image data be used directly? For the questions of camera and lens selection, in this chapter we will consider only systems that use a single camera with a fixed focal length lens. We briefly discuss the remaining questions below.
11.1.1 Camera Configuration
Perhaps the first decision to be made when constructing a vision-based control system is where to place the camera. There are essentially two options: the camera can be mounted in a fixed location in the workspace or it can be attached to the robot. These are often referred to as fixed-camera and eye-in-hand configurations, respectively.
With a fixed-camera configuration, the camera is positioned so that it can observe the manipulator and any objects to be manipulated. There are several advantages to this approach. Since the camera position is fixed, the field of view does not change as the manipulator moves. The geometric relationship between the camera and the workspace is fixed, and can be calibrated offline. One disadvantage to this approach is that as the manipulator moves through the workspace, it can occlude the camera’s field of view. This can be particularly important for tasks that require high precision. For example, if an insertion task is to be performed, it may be difficult to find a position from which the camera can view the entire insertion task without occlusion from the end effector. This problem can be ameliorated to some extent by using multiple cameras, but for robots performing tasks in dynamic or cluttered environments, it may be difficult, or even impossible to determine a set of fixed camera positions that can view all relevant aspects of the scene throughout the complete task execution.
With an eye-in-hand system1, the camera is often attached to the manipulator above the wrist so that the motion of the wrist does not affect the camera motion. In this way, the camera can observe the motion of the end effector at a fixed resolution and without occlusion as the manipulator moves through the workspace. One difficulty that confronts the eye-in-hand configuration is that the geometric relationship between the camera and the workspace changes as the manipulator moves. The field of view can change drastically for even small motion of the manipulator, particularly if the link to which the camera is attached experiences a change in orientation.
For either the fixed-camera or eye-in-hand configuration, motion of the manipulator will produce changes in the images obtained by the camera. The analysis of the relationships between manipulator motion and changes in the image for the two cases is similar mathematically, and in this text we will consider only the case of eye-in-hand systems.
11.1.2 Image-Based vs. Position-Based Approaches
There are two basic ways to approach the problem of vision-based control, and these are distinguished by the way in which the data provided by the vision system are used. These two approaches can also be combined in various ways to yield what are known as partitioned control schemes.
The first approach to vision-based control is known as position-based visual servo control. With this approach, the vision data are used to build a partial 3D representation of the world. For example, if the task is to grasp an object, a model of the imaging geometry (such as the pinhole camera model discussed below) can be used to determine the 3D coordinates of the grasp points relative to the camera coordinate frame. For eye-in-hand systems, if these 3D coordinates can be obtained in real time they can be used to determine a motion that will reduce the error between the current and desired end-effector pose. The main difficulties with position-based methods are related to the difficulty of building the 3D representation in real time. For example, these methods tend not to be robust with respect to errors in camera calibration. An additional problem arises from the fact that the error signal used by the control algorithm is defined in terms of the end-effector pose. It is possible that a motion could reduce this pose error while simultaneously inducing camera motion that could, for example, cause the object of interest to leave the camera field of view.
A second method known as image-based visual servo control uses the image data directly to control the robot motion. An error function is defined in terms of quantities that can be directly measured in an image (for example, image coordinates of points or the orientations of lines in an image) and a control law is constructed that maps this error directly to robot motion. Typically, relatively simple control laws are used to map the image error to robot motion. We will describe image-based control in some detail in this chapter.
It is possible to combine multiple approaches, using different control algorithms to control different aspects of the camera motion. For example, we might use a position-based approach to control the orientation of the camera while using an image-based approach to control its position. Such methods essentially partition the degrees of freedom of the camera motion into disjoint sets, and are thus known as partitioned methods. We briefly describe one particular partitioned method in Section 11.7.
11.2 Computer Vision for Vision-Based Control
Many types of images have been used for controlling robot motion, including grayscale images, color images, ultrasound images, and range images. In this chapter, we restrict our attention to the case of two-dimensional grayscale images. Such an image is formed by using a lens to focus light onto a two-dimensional sensor, the most common of which are CMOS2 and charge-coupled device (CCD) sensors. The sensor consists of a two-dimensional array of individual sensing elements, each of which corresponds to an image pixel (derived from the term picture element), whose value corresponds to the intensity of the light incident on the particular sensing element. A digital camera is able to transmit these values directly to a computer, for example via a USB interface, where the image can be represented as a two-dimensional array of intensity values. These intensity values could be represented as integers, 8-bit unsigned integers (implying that pixel values are integers ranging from 0 to 255), floating point numbers, or even double precision floating point numbers.
A typical image can contain several megabytes of data; however, the amount of data contained in an image often far exceeds the information content of the image. For this reason, most vision-based control algorithms begin by identifying useful features in the image, typically defined in terms of pixel values in a small region of the image. To be useful for vision-based control, features should be relatively easy to detect, have desirable robustness properties (e.g., invariance with respect to scale, orientation of the camera, lighting, etc.), and be distinctive relative to possible image content (i.e., they should be uniquely recognizable in an image). If features are well chosen, they can be used for object identification, 3D scene reconstruction, or for tracking specific objects as the camera (or the object) moves. For the case of vision-based control, feature identification and tracking are essential steps in relating the changes in an image to the corresponding camera motion.
In the remainder of this section we first describe the geometry of image formation and then discuss approaches to image feature detection and tracking. Later, by investigating how specific features are affected by camera motion, we will derive specific vision-based control algorithms.
11.2.1 The Geometry of Image Formation
For vision-based control, it is typically not necessary to explicitly consider the photometric aspects of image formation, such as issues related to focus, depth of field, or lens distortions. Therefore, in this chapter we describe only the geometry of the image formation process.
Figure 11.1 illustrates the basic geometry of the image formation process under the pinhole lens model, a commonly used approximation for the imaging process. With this model, the lens is considered to be an ideal pinhole that is located at the focal center of the lens, also referred to as the center of projection. Light rays pass through this pinhole, intersecting the image plane3.

Figure 11.1 The camera coordinate frame is placed at distance λ behind the image plane, with z-axis perpendicular to the image plane and aligned with the optical axis of the lens.
We define a camera-centric coordinate system as follows. The image plane is the plane that contains the sensing array. The x-axis and y-axis form a basis for the image plane and are typically taken to be parallel to the horizontal and vertical axes (respectively) of the sensing array. The z-axis is perpendicular to the image plane and aligned with the optical axis of the lens, that is, it passes through the focal center of the lens. The origin of the camera frame is located at a distance λ behind the image plane, referred to as the focal length of the camera lens. The point at which the optical axis intersects the image plane is known as the principal point. With this assignment of the camera frame, any point in the image plane will have coordinates (u, v, λ). Thus, we can use (u, v) to parameterize the image plane, and we will refer to (u, v) as image-plane coordinates.
Let P be a point in the world with coordinates (x, y, z) relative to the camera frame, and let p denote the projection of P onto the image plane with coordinates (u, v, λ). Under the pinhole model, the points P, p, and the origin of the camera frame will be collinear, as shown in Figure 11.1. Thus, for some unknown positive constant k we have
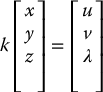
which can be rewritten as the system of equations
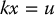
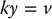
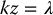
Equation (11.3) implies that k = λ/z, which can be substituted into Equations (11.1) and (11.2) to obtain
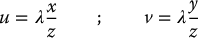
These are the well-known equations for perspective projection
Note that the perspective projection equations are expressed in the camera coordinate frame. If coordinates are to be specified with respect to some other frame, for example the end-effector frame or the inertial frame, it is necessary to know the coordinate transformation that relates the camera frame to this other frame. This is achieved by camera calibration, which is discussed in Appendix E. It should also be noted that pixels in a digital image have discrete integer coordinates, referred to as pixel coordinates. The relationship between pixel coordinates and image-plane coordinates is also discussed in Appendix E.
Example 11.1. (Distance and Scale).
Consider a camera viewing a square table from above, such that the image plane is parallel to the tabletop, and the camera frame axes are parallel to the sides of the table, as shown in Figure 11.2. Let the corners of the left-most edge of the table have coordinates (x, y1, z) and (x, y2, z) w.r.t. the camera frame. Note that the two corners share a common x-coordinate because the y-axis of the camera is parallel to the table edge, and share a common z-coordinate because the table is parallel to the image plane. In the image, the length of the edge is easily computed as
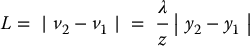
and the area of the tabletop in the image is given by
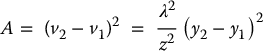
These two relationships illustrate two effects of perspective projection, namely that distance between image points decreases linearly with inverse-depth, and area occupied in an image decreases with the square of the inverse-depth. In vision-based control, these effects often manifest as gain terms in the feedback control design.

Figure 11.2 Camera viewing a table from overhead, as in Example 11.1.
Example 11.2. (Vanishing Points).
Consider an environment that contains a collection of parallel lines such as shown in Figure 11.3. Suppose the equations for these lines (in world coordinates) are given by
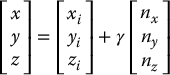
in which (xi, yi, zi)T is some point on the ith line, and n = (nx, ny, nz)T is the direction of the lines, both specified relative to the camera frame, and γ is a parameter that determines distance along the line. Although the lines are parallel, due to the effects of perspective projection, the images of these lines will intersect (except when the lines are parallel to the image plane). This intersection point is known as the vanishing point. To find the vanishing point, one merely need note that in projective geometry two parallel lines intersect at a point that lies on the line at infinity4. Thus, we can find the vanishing point by examining the case where γ → ∞.
If we let (u∞, v∞) denote the image-plane coordinates for the vanishing point, we have
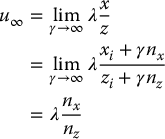
and by similar reasoning,
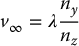
Note that when nz = 0 the lines are parallel to the image plane, and the images of the lines do not have a finite point of intersection.

Figure 11.3 The boundaries of the various sidewalks in this scene are all parallel, and therefore have a common vanishing point in the image.
11.2.2 Image Features
Image features are defined by patterns that can be detected in an image, and that have an associated set of measurable attributes. As an example, object corners are often easy to detect in images using specially designed algorithms known as corner detectors; their attributes might include the image coordinates of the corner and the angle between the two edges incident at the corner.
One of the basic problems in visual servo control is to track a set of features through a sequence of images, and to infer things about camera motion from the corresponding changes in the attributes of those features. Thus, to be useful for visual servo control, an image feature should have two properties. First, the feature should convey geometric information about the position and orientation of the camera relative to its environment, and camera motion should correspond in a well-defined way to changes in the attributes of the feature. Second, the feature should be easy to detect and track in an image sequence. For example, if an object corner is used as a feature, it should be easy to detect in an image, and to track in successive frames of an image sequence.
The computer vision literature is replete with examples of features, including features that are based directly on intensity values, features that are based on image gradient information, features that are based on aggregate properties of image regions, and many more. Rather than provide a catalog of possible features, below we focus on the class of gradient-based features. Even in this restricted case, we do not develop the full details, but rather we present a conceptual introduction, leaving details of implementation to the reader. This should not be a significant burden, as numerous feature detection algorithms have been implemented in open-source computer vision software packages that are readily accessible.
Gradient-Based Features
Even though an image consists of a discrete set of pixels whose intensity values are represented as unsigned integers, when defining image features it is often convenient to treat the image as a continuous plane, and to consider the image intensity to be a real-valued function,  , that maps points on this image plane to their corresponding intensity values. Using this approach, we can define image features in terms of the local structure of the function I. The gradient of a function provides a good approximation to its local structure, and therefore a number of image features have been defined in terms of the image gradient, ∇I.
, that maps points on this image plane to their corresponding intensity values. Using this approach, we can define image features in terms of the local structure of the function I. The gradient of a function provides a good approximation to its local structure, and therefore a number of image features have been defined in terms of the image gradient, ∇I.
Perhaps the simplest image feature that can be defined in this manner is an image edge. If an image contains an edge, there will be a sharp change in the image intensity in the direction perpendicular to the edge. This gives rise to a gradient with large magnitude. Many edge detection algorithms compute discrete approximations to the image gradient, and classify a pixel as belonging to an edge when the magnitude of the gradient exceeds a given threshold at that pixel. The Sobel edge detector is a well-known method that applies weighted local averaging to a first-order difference approximation of the image gradient. Figure 11.4(a) shows an intensity image, and Figure 11.4(b) shows the result of applying the Sobel operator to the image.

Figure 11.4 The Sobel edge detector applies local image smoothing and a discrete approximation of the gradient operator at each pixel. (a) An intensity image. (b) The result of applying the Sobel operator to the image.
Edges are not particularly good features for visual servo control, because they give good localization information only in the direction perpendicular to the edge. For example, if we slide a small window along an edge in an image, the sub-image contained in that window changes very little in appearance. Thus, edges do not provide good localization information in directions parallel to the edge. Corners, however, have good localization properties, since at a corner the intensity changes significantly in directions that are parallel to, as well as perpendicular to, the feature. Stated another way, if an image contains a corner located at (u0, v0), a window centered at (u0, v0) will be significantly different from windows centered at (u0 + δu, v0 + δv) for small values of δu and δv. This observation is the basis for a number of corner detection algorithms.
A common way to evaluate the similarity of two windows that are offset from one another is to evaluate the integral of squared differences between the two windows. Consider a reference window of size 2ℓ × 2ℓ centered at (u0, v0) and a 2ℓ × 2ℓ target window centered at (u0 + δu, v0 + δv), as shown in Figure 11.5. We can evaluate the similarity of these two windows by integrating the squared difference between the intensity value of each point in the reference image and its corresponding point in the shifted image
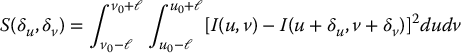

Figure 11.5 The reference window is centered at (u0, v0), and the target window is centered at (u0 + δu, v0 + δv). For each point xr in the reference image, the squared-difference integral computes a difference for its corresponding point xt in the target image.
We can approximate the integrand in Equation (11.5) in terms of the image gradient ∇I = (Iu, Iv)T. Applying the Taylor series expansion for I about the point (u, v) we obtain
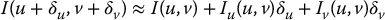
and substituting this into Equation (11.5) we obtain
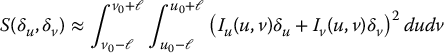
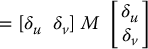
in which M, called the second moment matrix, or structure tensor, is given by
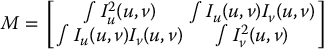
Note that M is defined in terms of the image gradient at the point (u, v), and does not depend on δu or δv. Thus, M is a gradient-based feature descriptor that characterizes the local variation of the image intensity about the image point (u, v).
Since M is a symmetric positive semi-definite matrix (this follows from the fact that the integrand in Equation (11.7) is positive, except for the degenerate case in which I is constant over the window), Equation (11.8) is a quadratic form that defines an ellipse, and which can be characterized by its eigenvalues λ1 ⩾ λ2 (see, for example, Section 4.12). If λ1 and λ2 are both large, then there is significant variation in all directions, indicating the likelihood of a corner at the point (u0, v0). If λ1 is large and λ2 ≈ 0, then there is little variation along one direction, corresponding to an edge at the point (u0, v0). If both λ1 ≈ 0 and λ2 ≈ 0, then there is very little variation in the image around the point (u0, v0), indicating an absence of useful features.
For images comprised of discrete pixels, the matrix M is computed using summations over discrete pixel windows, for an appropriate discrete approximation to the image gradient.
Remark 11.1.
Features that can be described using variations of the structure tensor described above are at the heart of several well-known feature detectors, including the Harris and Shi-Tomasi feature detectors. The histogram of oriented gradients (HOG) is a gradient-based feature descriptor that does not rely on the structure tensor.
Feature Detection and Tracking
The two problems of feature detection and feature tracking are different but closely related. The feature detection problem is to find a particular feature in an image, given no prior knowledge about the location of the feature. In contrast, the feature tracking problem is to find a feature in the current image, assuming that it has been detected in the previous image. In the latter case, the feature location in the previous image, along with any known information about camera motion, can be used to guide the feature detection in the current image. If a model of camera motion is given (even an uncertain model), the tracking problem can be approached using standard techniques from estimation theory, such as the Kalman filter or extended Kalman filter (EKF). With this approach, the position and orientation of the feature (or the camera) can be considered as the state, and the process and observation models are derived using the camera motion model and image formation model. While numerous methods for feature tracking have been developed, these lie beyond the scope of this text.
11.3 Camera Motion and the Interaction Matrix
Once we have chosen a set of features and designed a feature tracker, it is possible detect a feature as it moves in an image sequence, and to compute the values of its various attributes in each image frame. For vision-based control, it is useful to relate camera motion to the changes in these feature attributes. In this section, we develop the mathematical formulation for this relationship.
Recall the inverse velocity problem discussed in Chapter 4. Even though the inverse kinematics problem is difficult to solve and often ill-posed, the inverse velocity problem is typically fairly easy to solve: one merely inverts the manipulator Jacobian matrix, assuming the Jacobian is nonsingular. This can be understood mathematically by noting that while the inverse kinematic equations represent a nonlinear mapping between possibly complicated geometric spaces, for a given configuration q, the mapping of velocities is a linear map between linear subspaces. For example, for the two-link planar arm, the inverse kinematic equations map an end-effector position,  to the joint variables (θ1, θ2) that lie on the surface of a torus; however the inverse velocity relationship maps a velocity vector in
to the joint variables (θ1, θ2) that lie on the surface of a torus; however the inverse velocity relationship maps a velocity vector in  to a velocity that lies in the tangent plane to the torus at (θ1, θ2). Likewise, the relationship between the camera velocity and the corresponding differential changes in the attributes of image features is a linear mapping between linear subspaces. We will now give a more rigorous explanation of this basic idea.
to a velocity that lies in the tangent plane to the torus at (θ1, θ2). Likewise, the relationship between the camera velocity and the corresponding differential changes in the attributes of image features is a linear mapping between linear subspaces. We will now give a more rigorous explanation of this basic idea.
Let s(t) denote the vector of feature attributes that can be measured in an image. Its derivative  is referred to as an image feature velocity. For example, if a single image point is used as a feature, we could consider the image-plane coordinates of the point as a feature attribute, giving
is referred to as an image feature velocity. For example, if a single image point is used as a feature, we could consider the image-plane coordinates of the point as a feature attribute, giving
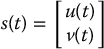
In this case  would be the image plane velocity of the image point.
would be the image plane velocity of the image point.
The image feature velocity is linearly related to the camera velocity. Let the camera velocity ξ consist of linear velocity5 v and angular velocity ω
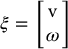
so that the origin of the camera frame is moving with linear velocity v and the camera frame is rotating about the axis ω, which passes through the origin of the camera frame. There is no difference between ξ as used here and as used in Chapter 4; in each case, ξ encodes the linear and angular velocity of a moving frame. In Chapter 4 the frame was attached to the end effector while here it is attached to the moving camera.
The relationship between  and ξ is given by
and ξ is given by
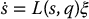
Here, the matrix L(s, q) is known as the interaction matrix. The interaction matrix is a function of both the configuration of the robot, as was also true for the manipulator Jacobian described in Chapter 4, and of the image feature values s.
The interaction matrix L is also called the image Jacobian matrix. This is due, at least in part, to the analogy that can be drawn between the manipulator Jacobian discussed in Chapter 4 and the interaction matrix. In each case, a velocity ξ is related to the differential change in a set of parameters, either joint velocities or image feature velocities, by a linear transformation. Strictly speaking, the interaction matrix is not a Jacobian matrix, since ξ is not actually the derivative of some set of pose parameters. However, using techniques analogous to those used to develop the analytic Jacobian in Section 4.8, it is straightforward to construct an actual Jacobian matrix that represents a linear transformation from the derivatives of a set of pose parameters to the image feature velocities, which are derivatives of the image feature attributes.
The specific form of the interaction matrix depends on the features that are used to define s. The simplest features are coordinates of points in the image, and we will focus our attention on this case.
11.4 The Interaction Matrix for Point Features
In this section we derive the interaction matrix for the case of a moving camera observing a point that is fixed in space. This scenario is useful for postioning a camera relative to some object that is to be manipulated. For example, a camera can be attached to a manipulator that will be used to grasp a stationary object. Vision-based control can then be used to bring the manipulator to a grasping configuration that may be defined in terms of image features. In Section 11.4.4 we extend the development to the case of multiple feature points.
At time t, the orientation of the camera frame is given by a rotation matrix R0c = R(t), which specifies the orientation of the camera frame relative to the fixed frame. We denote by o(t) the position of the origin of the camera frame relative to the fixed frame. We denote by P the fixed point in the workspace, and by s = [u, v]T the feature vector corresponding to the projection of P in the image (see Figure 11.1).
Our goal is to derive the interaction matrix L that relates the velocity of the camera ξ to the derivatives of the coordinates of the projection of the point in the image  . We begin by finding an expression for the velocity of the point P relative to the moving camera. We then use the perspective projection equations to relate this velocity to the image velocity
. We begin by finding an expression for the velocity of the point P relative to the moving camera. We then use the perspective projection equations to relate this velocity to the image velocity  . Finally, after a bit of algebraic manipulation we arrive to the interaction matrix that satisfies
. Finally, after a bit of algebraic manipulation we arrive to the interaction matrix that satisfies  .
.
11.4.1 Velocity Relative to a Moving Frame
We now derive an expression for the velocity of a fixed point in the world frame relative to a moving camera frame. We denote by  the coordinates of P relative to the world frame. Note that
the coordinates of P relative to the world frame. Note that  does not vary with time, since P is fixed with respect to the world frame. If we denote by pc(t) the coordinates of P relative to the moving camera frame at time t, using Equation (2.58) we have
does not vary with time, since P is fixed with respect to the world frame. If we denote by pc(t) the coordinates of P relative to the moving camera frame at time t, using Equation (2.58) we have
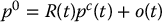
Thus, at time t we can solve for the coordinates of P relative to the camera frame by
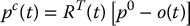
Now, to find the velocity of the point P relative to the moving camera frame we merely differentiate this equation, as was done in Chapter 4. We will drop the explicit reference to time in these equations to simplify notation. Using the product rule for differentiation we obtain
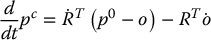
From Equation (4.18) we have  , and thus
, and thus  . This allows us to write Equation (11.13) as
. This allows us to write Equation (11.13) as
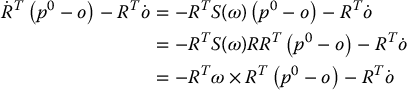
In this equation the rotation matrix RT is applied to three vectors, yielding three new vectors whose coordinates are expressed with respect to the camera frame. From Equation (11.12) we see that  . The vector ω gives the angular velocity vector for the moving frame in coordinates expressed with respect to the fixed frame, that is, ω = ω0. Therefore, RTω = Rc0ω0 = ωc gives the angular velocity vector for the moving frame in coordinates expressed with respect to the moving frame. Finally, note that
. The vector ω gives the angular velocity vector for the moving frame in coordinates expressed with respect to the fixed frame, that is, ω = ω0. Therefore, RTω = Rc0ω0 = ωc gives the angular velocity vector for the moving frame in coordinates expressed with respect to the moving frame. Finally, note that  . Using these conventions we can immediately write the equation for the velocity of P relative to the moving camera frame
. Using these conventions we can immediately write the equation for the velocity of P relative to the moving camera frame
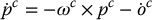
Relating this to the velocity ξ we see that ωc is the angular velocity of the camera frame expressed relative to the moving camera frame, and  is the linear velocity v of the camera frame, also expressed relative to the moving camera frame. It is interesting to note that the velocity of a fixed point relative to a moving frame is merely − 1 times the velocity of a moving point relative to a fixed frame.
is the linear velocity v of the camera frame, also expressed relative to the moving camera frame. It is interesting to note that the velocity of a fixed point relative to a moving frame is merely − 1 times the velocity of a moving point relative to a fixed frame.
Example 11.3. (Camera Motion in the Plane).
Consider a camera whose optical axis is parallel to the world z-axis. If the camera motion is constrained to rotation about the optical axis and translation parallel to the x-y plane, we have
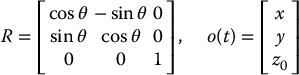
in which z0 is the fixed height of the camera frame relative to the world frame. This gives
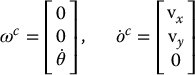
If the point P has coordinates (x, y, z) relative to the camera frame, we have
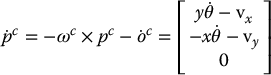
11.4.2 Constructing the Interaction Matrix
Using Equation (11.14) and the equations of perspective projection, it is not difficult to derive the interaction matrix for point features. To simplify notation, we define the coordinates for P relative to the camera frame as pc = [x, y, z]T. By this convention, the velocity of P relative to the moving camera frame is merely the vector  . We will denote the coordinates for the angular velocity vector by ωc = [ωx, ωy, ωz]T = RTω, where ω is the camera angular velocity expressed relative to the world coordinate frame. To further simplify notation, we assign coordinates
. We will denote the coordinates for the angular velocity vector by ωc = [ωx, ωy, ωz]T = RTω, where ω is the camera angular velocity expressed relative to the world coordinate frame. To further simplify notation, we assign coordinates  . Using these conventions, we can write Equation (11.14) as
. Using these conventions, we can write Equation (11.14) as
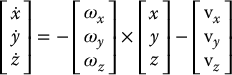
which can be written as the system of three equations
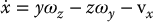
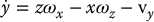
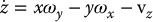
Since u and v are the image coordinates of the projection of P in the image, using Equation (11.4), we can express x and y as
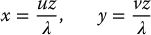
Substituting these into Equations (11.15)–(11.17) we obtain
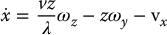
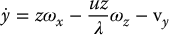
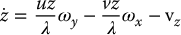
These equations express the velocity  in terms of the image coordinates u, v, the depth z of the point P, and the angular and linear velocity of the camera. We will now find expressions for
in terms of the image coordinates u, v, the depth z of the point P, and the angular and linear velocity of the camera. We will now find expressions for  and
and  and then combine these with Equations (11.18)–(11.20).
and then combine these with Equations (11.18)–(11.20).
Using the quotient rule for differentiation with the equations of perspective projection we obtain
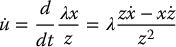
Substituting Equations (11.18) and (11.20) into this expression gives
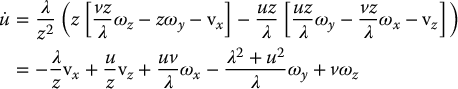
We can apply the same technique for  to obtain
to obtain
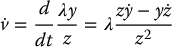
and substituting Equations (11.19) and (11.20) into this expression gives
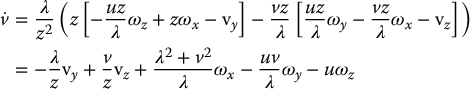
Equations (11.21) and (11.22) can be combined and written in matrix form as
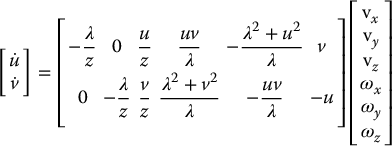
The matrix in Equation (11.23) is the interaction matrix for a point. To make explicit its dependence on u, v, and z, Equation (11.23) is often written as

Example 11.4. (Camera Motion in the Plane).
Returning to the situation described in Example 11.3. Suppose that the point P has coordinates p0 = [xp, yp, 0]T relative to the world frame. Relative to the camera frame, P has coordinates given by
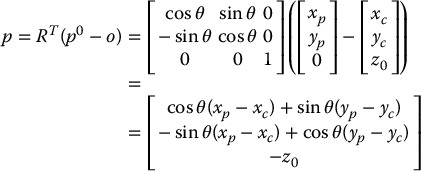
The image coordinates for P are thus given by
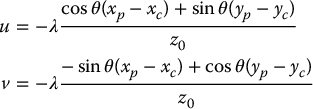
These can be substituted into Equation (11.24) to yield
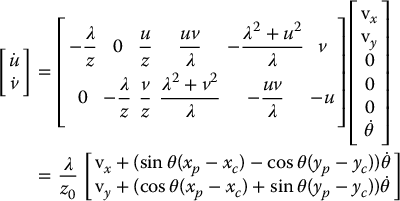
11.4.3 Properties of the Interaction Matrix for Points
Equation (11.23) can be decomposed as
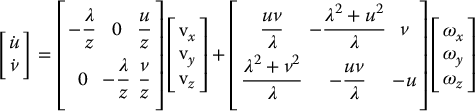
which can be written as
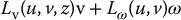
in which Lv(u, v, z) contains the first three columns of the interaction matrix, and is a function of both the image coordinates of the point and its depth, while Lω(u, v) contains the last three columns of the interaction matrix, and is a function of only the image coordinates of the point, that is, it does not depend on depth. This can be particularly beneficial in real-world situations when the exact value of z may not be known. In this case, errors in the value of z merely cause a scaling of the matrix Lv(u, v, z), and this kind of scaling effect can be compensated for by using fairly simple control methods. This kind of decomposition is at the heart of the partitioned method that we discuss in Section 11.7.
For a camera with six degrees of freedom (e.g., a camera attached to the end effector of a six-link arm), we have  , while only the two values u and v are observed in the image. Thus, one would expect that not all camera motions cause observable changes in the image. More precisely,
, while only the two values u and v are observed in the image. Thus, one would expect that not all camera motions cause observable changes in the image. More precisely,  and therefore has a null space of dimension 4. Therefore, the system
and therefore has a null space of dimension 4. Therefore, the system
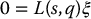
has solution vectors ξ that lie in a four-dimensional subspace of  . For the case of a single point, it can be shown (Problem 11–12) that the null space of the interaction matrix given in Equation (11.23) is spanned by the four vectors
. For the case of a single point, it can be shown (Problem 11–12) that the null space of the interaction matrix given in Equation (11.23) is spanned by the four vectors
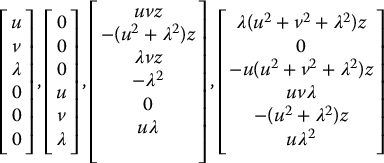
The first two of these vectors have particularly intuitive interpretations. The first corresponds to motion of the camera frame along a line that contains both the lens focal center and the point P. Such lines are called projection rays. The second corresponds to rotation of the camera frame about a projection ray that contains P.
11.4.4 The Interaction Matrix for Multiple Points
It is straightforward to generalize the development above to the case in which several points are used to define the image feature vector. Consider the case for which the feature vector consists of the coordinates of n image points. Here, the ith feature point has an associated depth zi and we define the feature vector s and the vector of depth values z by
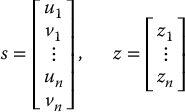
For this case, the composite interaction matrix Lc that relates camera velocity to image feature velocity is a function of the image coordinates of the n points and also of the n depth values, is obtained by stacking the n interaction matrices for the individual feature points,

Thus, we have  . Since each image point gives rise to two feature values (the u, v coordinates of the point), three image points provide six feature values, which is sufficient to solve for ξ given the image measurements
. Since each image point gives rise to two feature values (the u, v coordinates of the point), three image points provide six feature values, which is sufficient to solve for ξ given the image measurements  , provided that Lc is full rank.
, provided that Lc is full rank.
11.5 Image-Based Control Laws
With image-based control, the goal configuration is defined by a desired configuration of image features, denoted by  , where the dimension k depends on the task. The image error function is then given by
, where the dimension k depends on the task. The image error function is then given by
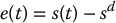
The image-based control problem is to find a mapping from this error function to a commanded camera motion. As we have seen in previous chapters, there are a number of control approaches that can be used to determine the joint-level inputs to achieve a desired trajectory. Therefore, in this chapter we will treat the manipulator as a kinematic positioning device, that is, we will ignore manipulator dynamics and develop controllers that compute desired end-effector trajectories. The underlying assumption is that these trajectories can then be tracked by a lower level manipulator controller.
Example 11.5 (A Simple Positioning Task).
Visual servo tasks are often specified by defining the desired location of a set of features in an image. Consider the task of positioning a camera relative to a pile of books, as shown in Figure 11.6. For this example, we define the task by specifying the location of four features, sd1, s2d, sd3, s4d, in the goal image, as shown in Figure 11.6(a). Figure 11.6(b) shows an initial image, and the corresponding error vectors for each of the four features. An image-based control law will map these error vectors to a corresponding camera motion that will reduce the error.

Figure 11.6 The goal image is shown on the left. When the camera reaches the desired configuration, the features sd1, s2d, sd3, s4d will be located as shown in this image. The initial image is shown on the right, along with four error vectors that correspond to the four image features.
The most common approach to image-based control is to compute a desired camera velocity ξ and use this as the control input. Relating image feature velocities to the camera velocity is typically done by solving  for ξ, which gives the camera velocity that will produce a desired value for
for ξ, which gives the camera velocity that will produce a desired value for  . In some cases, this can be done simply by inverting the interaction matrix, but in other cases the pseudoinverse must be used. Below we describe various pseudoinverses of the interaction matrix and then explain how these can be used to construct an image-based control law.
. In some cases, this can be done simply by inverting the interaction matrix, but in other cases the pseudoinverse must be used. Below we describe various pseudoinverses of the interaction matrix and then explain how these can be used to construct an image-based control law.
11.5.1 Computing Camera Motion
For the case of k feature values and m components of the camera body velocity ξ, we have  . In general we will have m = 6, but in some cases we may have m < 6, for example if the camera is attached to a SCARA arm used to manipulate objects on a moving conveyor. When L is full rank (i.e., when rank(L) = min (k, m)), it is possible to compute ξ for a given
. In general we will have m = 6, but in some cases we may have m < 6, for example if the camera is attached to a SCARA arm used to manipulate objects on a moving conveyor. When L is full rank (i.e., when rank(L) = min (k, m)), it is possible to compute ξ for a given  . There are three cases that must be considered: k = m, k > m, and k < m.
. There are three cases that must be considered: k = m, k > m, and k < m.
- When k = m and L is full rank, we have
 . This is the case when the number of feature values is equal to the number of degrees of freedom for the camera.
. This is the case when the number of feature values is equal to the number of degrees of freedom for the camera. -
When k < m, L− 1 does not exist, and the system is underconstrained. In the visual servo application, this implies that we are not observing enough feature velocities to uniquely determine the camera motion ξ, that is, there are certain components of the camera motion that cannot be observed (namely, those that lie in the null space of L). In this case we can compute a solution given by
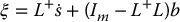
where L+ is the right pseudoinverse for L, given by
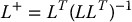
Im is the m × m identity matrix, and
 is an arbitrary vector. Note the similarity between this equation and Equation (4.112) which gives the solution for the inverse velocity problem (that is, solving for joint velocities to achieve a desired end-effector velocity) for redundant manipulators.
is an arbitrary vector. Note the similarity between this equation and Equation (4.112) which gives the solution for the inverse velocity problem (that is, solving for joint velocities to achieve a desired end-effector velocity) for redundant manipulators.In general, for k < m, (I − LL+) ≠ 0, but all vectors of the form (I − LL+)b lie in the null space of L, which implies that those components of the camera velocity that are unobservable lie in the null space of L. If we let b = 0, we obtain the value for ξ that minimizes the norm
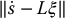
- When k > m and L is full rank, we will typically have an inconsistent system, especially when the feature values s are obtained from measured image data. In the visual servo application, this implies that we are observing more feature velocities than are required to uniquely determine the camera motion ξ. In this case the rank of the null space of L is zero, since the dimension of the column space of L equals rank(L). In this situation, we can use the least squares solution
(11.26)in which we use the left pseudoinverse, which is given by
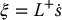 (11.27)
(11.27)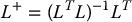
11.5.2 Proportional Control Schemes
Lyapunov theory (see Appendix C) can be used to analyze the stability of dynamical systems, but it can also be used to aid in the design of stable control systems. Consider again the visual servo problem given by
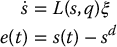
and define a candidate Lyapunov function as
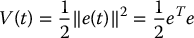
Note that this choice of V is a valid candidate Lyapunov function only if e ≠ 0 for every non-goal configuration (this condition is not satisfied, for example, when there is a nontrivial null space for L in a neighborhood of e = 0). The derivative of this function is
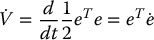
Thus, if we could design a controller such that
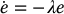
with λ > 0 we would have
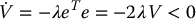
and this would ensure asymptotic stability of the closed-loop system. In fact, if we could design such a controller, we would have exponential stability, which ensures that the closed-loop system is asymptotically stable even under small perturbations, for example, small errors in camera calibration.
For the case of visual servo control, it is often possible to design such a controller. In the case of sd a constant6, the derivative of the error function is given by
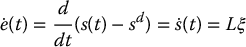
and substituting this into Equation (11.28) we obtain
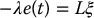
If k = m and L has full rank, then L− 1 exists, and we have
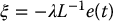
and the system is exponentially stable.
When k > m we obtain the control
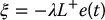
with L+ = (LTL)− 1LT. Unfortunately, in this case we do not obtain exponential stability. To see this, consider again the Lyapunov function given above. We have
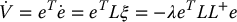
But in this case, the matrix LL+ is only positive semidefinite, not positive definite, and therefore we cannot demonstrate asymptotic stability by Lyapunov theory. This follows because  , and since k > m, it has a nonzero nullspace. This follows since rank(L) = min (k, m) < k implies that L has at most m < k linearly independent columns, and therefore there must exist some linear combination of columns ∑iαiLi = 0 such that not all αi = 0. The corresponding vector [α1…αk]T lies in the null space of L. Therefore, eLL+e = 0 for certain values of e, and we can demonstrate only stability, not asymptotic stability.
, and since k > m, it has a nonzero nullspace. This follows since rank(L) = min (k, m) < k implies that L has at most m < k linearly independent columns, and therefore there must exist some linear combination of columns ∑iαiLi = 0 such that not all αi = 0. The corresponding vector [α1…αk]T lies in the null space of L. Therefore, eLL+e = 0 for certain values of e, and we can demonstrate only stability, not asymptotic stability.
Remark 11.2.
In practice, we will not know the exact value of L or L+ since these depend on knowledge of depth information that must be estimated by the computer vision system. In this case, we will have an estimate for the interaction matrix  and we can use the control
and we can use the control  . It is easy to show, by a proof analogous to the one above, that the resulting visual servo system will be stable when
. It is easy to show, by a proof analogous to the one above, that the resulting visual servo system will be stable when  is positive definite. This helps explain the robustness of image-based control methods to calibration errors in the computer vision system.
is positive definite. This helps explain the robustness of image-based control methods to calibration errors in the computer vision system.
11.5.3 Performance of Image-Based Control Systems
While the image-based control law described above performs well with respect to the image error, it can sometimes induce large camera motions that cause task failure, for example, if the required camera motion exceeds the physical range of the manipulator. Such a case is illustrated in Figure 11.7. For this example, the camera image plane is parallel to the plane that contains the four feature points. When the feature points reach their desired positions in the image, the pose of the camera will differ from its initial pose by a pure rotation about the camera’s z-axis. Figure 11.7(a) shows the image feature trajectories for the four feature points when image-based control is applied. As can be seen in the figure, the feature points move on straight lines to their goal positions in the image. Figure 11.7(b) shows the image feature errors for the four points; the errors converge exponentially to zero. Unfortunately, as can be seen in Figure 11.7(c), to achieve this performance the camera retreats by a full one meter along its z-axis. Such a large motion is not possible for most manipulators. Figure 11.7(d) shows the corresponding camera velocities. The velocities along and about the camera x- and y-axes are very small, but the linear velocity along camera z-axis varies significantly.

Figure 11.7 In (a) the desired feature point locations are shown in dark circles, and the initial feature locations are shown as unfilled circles. As can be seen in (a), when image-based control is used, the feature points move on straight-line trajectories in the image to the desired positions, while the image error decreases exponentially to zero, as shown in part (b). Unfortunately, the required camera motion includes a significant retreat along the camera z-axis, as illustrated in (c) and (d).
The most extreme version of this problem occurs when the effective camera motion is a rotation by π about the camera’s optical axis. This case is shown in Figure 11.8. In Figure 11.8(a) the feature points again move on straight-line trajectories in the image. However, in this case, these trajectories pass through the image center. This occurs only when the camera has retreated infinitely far along its z-axis. The corresponding camera position is shown in Figure 11.8(b).

Figure 11.8 The required camera motion is a rotation by π about the camera z-axis. In (a) the feature points move along straight-line trajectories in the image, but in (b) this requires the camera to retreat to z = −∞.
These two examples are special cases that illustrate one of the key problems that confront image-based visual servo systems. Such systems explicitly control the error in the image, but exert no explicit control over the trajectory of the camera. Thus, it is possible that the required camera motions will exceed the capabilities of the robot manipulator. Partitioned methods provide one way to cope with these problems, and we describe one such method in Section 11.7.
11.6 End Effector and Camera Motions
The output of a visual servo controller is a camera velocity ξc, typically expressed in coordinates relative to the camera frame. If the camera frame were coincident with the end-effector frame, we could use the manipulator Jacobian to determine the joint velocities that would achieve the desired camera motion as described in Section 4.11. In most applications, the camera frame is not coincident with the end-effector frame, but is rigidly attached to it. Suppose the two frames are related by the constant homogeneous transformation
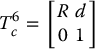
In this case, we can use Equation (4.81) to determine the required velocity of the end effector to achieve the desired camera velocity. This gives
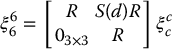
If we wish to express the end-effector velocity with respect to the base frame, we merely apply a rotational transformation to the two free vectors v6 and ω6, and this can be written as the matrix equation
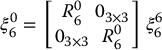
Example 11.6. (Eye-in-hand System with SCARA Arm).
Consider the camera system described in Example 11.4. Recall that in this example the camera motion was restricted to three degrees of freedom, namely,  . Suppose that this camera is attached to the end effector of a SCARA manipulator, such that the optical axis of the camera is aligned with the z-axis of the end-effector frame. In this case, we can express the orientation of the camera frame relative to the end-effector frame by
. Suppose that this camera is attached to the end effector of a SCARA manipulator, such that the optical axis of the camera is aligned with the z-axis of the end-effector frame. In this case, we can express the orientation of the camera frame relative to the end-effector frame by
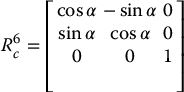
in which α gives the angle from x6 to xc. Let the origin of the camera frame relative to the end-effector frame be given by d6c = [10, 5, 0]T. The relationship between end effector and camera velocities is then given by
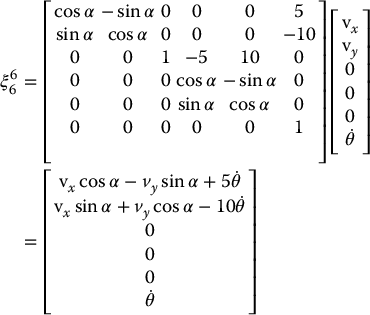
This can be used with the Jacobian matrix of the SCARA arm (derived in Chapter 4) to solve for the joint velocities required to achieve the desired camera motion.
11.7 Partitioned Approaches
Although image-based methods are versatile and robust to calibration and sensing errors, as discussed in Section 11.5.3 they sometimes fail when the required camera motion is large. Consider again the case illustrated in Figure 11.8. A pure rotation of the camera about the optical axis would cause each feature point to trace a trajectory in the image that lies on a circle, while image-based methods, in contrast, cause each feature point to move in a straight line from its current image position to its desired position. In the latter case, the induced camera motion is a retreat along the optical axis, in this case to z = −∞, at which point  and the controller fails. This problem is a consequence of the fact that image-based control does not explicitly take camera motion into account. Instead, image-based control determines a desired trajectory in the image feature space, and maps this trajectory, using the interaction matrix, to a camera velocity. One way to deal with such situations is to use a partitioned method.
and the controller fails. This problem is a consequence of the fact that image-based control does not explicitly take camera motion into account. Instead, image-based control determines a desired trajectory in the image feature space, and maps this trajectory, using the interaction matrix, to a camera velocity. One way to deal with such situations is to use a partitioned method.
Partitioned methods use the interaction matrix to control only a subset of the camera degrees of freedom, and use other methods to control the remaining degrees of freedom. Consider, for example Equation (11.23). We can write this equation as
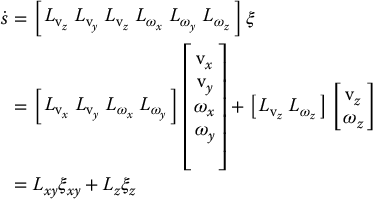
Here,  gives the component of
gives the component of  due to the camera motion along and rotation about the optical axis, while
due to the camera motion along and rotation about the optical axis, while  gives the component of
gives the component of  due to velocity along and rotation about the camera x- and y-axes.
due to velocity along and rotation about the camera x- and y-axes.
Equation (11.30) allows us to partition the control into two components, ξxy and ξz. Suppose that we have established a control scheme to determine the value ξz. Using an image-based method to find ξxy we would solve Equation (11.30) as
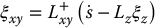
This equation has an intuitive explanation. The term − L+xyLzξz is the required value of ξxy to cancel the feature motion  . The control
. The control  gives the velocity along and rotation about the camera x- and y-axes that produce the desired
gives the velocity along and rotation about the camera x- and y-axes that produce the desired  once image feature motion due to ξz has been taken into account.
once image feature motion due to ξz has been taken into account.
If we use the Lyapunov design method described above, we set  , and obtain
, and obtain
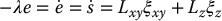
which leads to
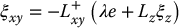
We can consider (λe + Lzξz) as a modified error that incorporates the original image feature error while taking into account the feature error that will be induced by the translation along and rotation about the optical axis due to ξz.
The only remaining task is to construct a control law to determine the value of ξz. To determine ωz, we can use the angle θij from the horizontal axis of the image plane to the directed line segment joining two feature points. For numerical conditioning it is advantageous to select the longest line segment that can be constructed from the feature points, allowing this choice to change during the motion as the feature point configuration changes. The value for such an ωz is given by
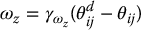
in which θdij is the desired value, and  is a scalar gain coefficient.
is a scalar gain coefficient.
We can use the apparent size of an object in the image to determine vz. Let σ2 denote the area of some polygon in the image. We define vz as
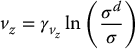
The advantages to using the apparent size as a feature are that it is a scalar that is invariant with respect to rotation about the optical axis (thus decoupling camera rotation from z-axis translation), and that it can be easily computed.
Figures 11.9 and 11.10 illustrate the performance of this partitioned controller for the case of desired rotation by π about the optical axis. Note in Figure 11.10 that the camera does not retreat (σ is constant), the angle θ monotonically decreases, and the feature points move in a circle. The feature coordinate error is initially increasing, unlike the classical image-based methods, in which feature error is monotonically decreasing.

Figure 11.9 For the case of pure image-based control, each feature point would move on a straight line from initial to goal location, as illustrated by the straight line segments in the figure; all feature points would pass simultaneously through the center of the circle in this case. Using the partitioned controller, the feature points move along the circle shown in the figure, until they reach their goal positions. The figure on the right shows the translational motion of the camera; note that motion along the z-axis is essentially zero.

Figure 11.10 The feature error trajectories for the motion illustrated in Figure 11.9, from top to bottom: error for the four feature points, error in σ, error in θ.
11.8 Motion Perceptibility
Recall that the notion of manipulability described in Section 4.12 gave a quantitative measure of the scaling from joint velocities to end-effector velocities. Motion perceptibility is an analogous concept that relates camera velocity to the velocity of features in the image. Intuitively, motion perceptibility quantifies the magnitude of changes to image features that result from motion of the camera.
Consider the set of all camera velocities ξ such that
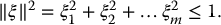
Suppose that there are redundant image features, that is, k > m. We may use Equation (11.26) to obtain
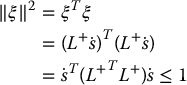
Now, consider the singular value decomposition of L (see Appendix B) given by
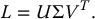
in which U and V are orthogonal matrices and  with
with
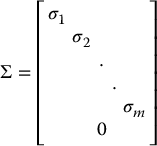
and the σi are the singular values of L and σ1 ⩾ σ2… ⩾ σm.
For this case, the pseudoinverse of the interaction matrix L+ is given by Equation (11.27). Using this with Equations (11.32) and (11.33) we obtain
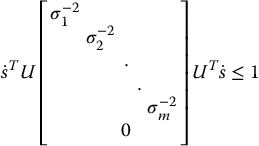
Consider the orthogonal transformation of  given by
given by
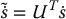
Substituting this into Equation (11.34) we obtain
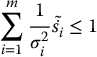
Equation (11.35) defines an ellipsoid in an m-dimensional space. We shall refer to this ellipsoid as the motion perceptibility ellipsoid. We may use the volume of the m-dimensional ellipsoid given in Equation (11.35) as a quantitative measure of the perceptibility of motion. The volume of the motion perceptibility ellipsoid is given by

in which K is a scaling constant that depends on m, the dimension of the ellipsoid. Because the constant K depends only on m, it is not relevant for the purpose of evaluating motion perceptibility, since m will be fixed for any particular problem. Therefore, we define the motion perceptibility, which we shall denote by ρ, as
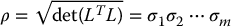
The motion perceptibility measure ρ has the following properties, which are direct analogs of properties derived for manipulability:
- In general, ρ = 0 holds if and only if rank(L) < min (k, m), that is, when L is not full rank.
- Suppose that there is some error in the measured visual feature velocity
 . We can bound the corresponding error in the computed camera velocity Δξ by
. We can bound the corresponding error in the computed camera velocity Δξ by
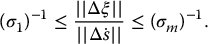
There are other quantitative methods that could be used to evaluate the perceptibility of motion. For example, in the context of feature selection the condition number for the interaction matrix, given by ‖L‖‖L− 1‖, could be used to select image features.
11.9 Summary
In this chapter, we introduced vision-based control, including an overview of those aspects of computer vision that are necessary to fully understand and implement vision-based control algorithms.
We began by discussing basic choices that confront the designer of a vision-based control scheme, distinguishing between fixed-camera and eye-in-hand systems (the latter being the focus of the current chapter), and between position-based and image-based control architectures. Image-based methods map image data directly to control signals, and are the primary focus of the chapter.
Our discussion of computer vision was limited to the geometric aspects of image formation. We presented perspective projection as a model for image formation. In this case, the projection onto the image plane of a point with coordinates (x, y, z) is given by the perspective projection equations
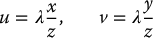
We then described how gradient information can be used to design a rudimentary corner detector.
Image-based visual servo control is a method for using an error measured in the image to directly control the motion of a robot. The key relationship exploited by all image-based methods is given by
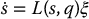
in which L(s, q) is the interaction matrix and s is a vector of measured image feature values. When a single image point is used as the feature, this relationship is given by
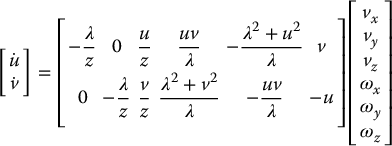
In image-based control the image error is defined by
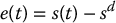
and by using the square of the error norm as a candidate Lyapunov function, we derive the control law
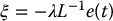
when the interation matrix is square and nonsingular or
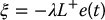
with L+ = (LTL)− 1LT when  and k > m.
and k > m.
In general, the camera coordinate frame and the end effector frame of the robot are not coincident. In this case, it is necessary to relate the camera velocity to the end effector velocity. This relationship is given by
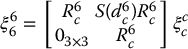
in which R6c and d6c specify the fixed relative orientation and position of the camera frame with respect to the end effector frame, and ξ6 and ξc denote the end effector and camera velocities, respectively.
In some cases, it is advantageous to use different control laws for the different degrees of freedom. In this chapter, we described one way to partition the control system using the relationship
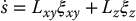
After defining two new image features, we controlled the z-axis translation and rotation using
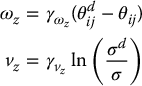
in which θij is the angle between the horizontal axis of the image plane and the directed line segment joining two feature points, σ2 is the area of a polygon in the image, and  and
and  are scalar gain coefficients.
are scalar gain coefficients.
Finally, we defined motion perceptibility as a property of visual servo systems that is analogous to the manipulability measure for manipulators. For k > m motion percpetibility is defined by
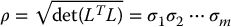
in which σi are the singular values of the interaction matrix.
Problems
- For a camera with focal length λ = 10, find the image plane coordinates for the 3D points whose coordinates with respect to the camera frame are given below. Indicate if any of these points will not be visible to a physical camera.
- (25, 25, 50)
- ( − 25, −25, 50)
- (20, 5, −50)
- (15, 10, 25)
- (0, 0, 50)
- (0, 0, 100)
- Repeat Problem 11–1 for the case when the coordinates of the points are given with respect to the world frame. Suppose the optical axis of the camera is aligned with the world x-axis, the camera x-axis is parallel to the world y-axis, and the center of projection has coordinates (0, 0, 100).
-
A stereo camera system consists of two cameras that share a common field of view. By using two cameras, stereo vision methods can be used to compute 3D properties of the scene. Consider stereo cameras with coordinate frames o1x1y1z1 and o2x2y2z2 such that
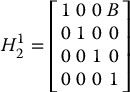
Here, B is called the baseline distance between the two cameras. Suppose that a 3D point P projects onto these two images with image plane coordinates (u1, v1) in the first camera and (u2, v2) in the second camera. Determine the depth of the point P.
- Show that the projection of a 3D line is a line in the image.
- Show that the vanishing points for all 3D horizontal lines must lie on the line v = 0 of the image plane.
-
Suppose the vanishing point for two parallel lines has the image coordinates (u∞, v∞). Show that the direction vector for the 3D line is given by
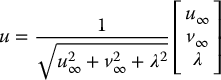
in which λ is the focal length of the imaging system.
- Two parallel lines define a plane. Consider a set of pairs of parallel lines such that the corresponding planes are all parallel. Show that the vanishing points for the images of these lines are collinear. Hint: let n be the normal vector for the parallel planes and exploit the fact that ui · n = 0 for the direction vector ui associated to the ith line.
-
A cube has twelve edges, each of which defines a line in three space. We can group these lines into three groups, such that in each of the groups there are four parallel lines. Let (a1, a2, a3), (b1, b2, b3), and (c1, c2, c3) be the direction vectors for these three sets of parallel lines. Each set of parallel lines gives rise to a vanishing point in the image. Let the three vanishing points be Va = (ua, va), Vb = (ub, vb), and Vc = (uc, cc), respectively.
- If C is the optical center of the camera, show that the three angles ∠VaCVb, ∠VaCVc and ∠VbCVc are each equal to
 . Hint: In the world coordinate frame, the image plane is the plane z = λ.
. Hint: In the world coordinate frame, the image plane is the plane z = λ. - Let ha be the altitude from Va to the line defined by Vb and Vc. Show that the plane containing both ha and the line through points C and Va is orthogonal to the line defined by Vb and Vc.
-
Let ha be the altitude from Va to the line defined by Vb and Vc, hb the altitude from Vb to the line defined by Va and Vc, and hc the altitude from Vc to the line defined by Va and Vb. We define the following three planes:
- Pa is the plane containing both ha and the line through points C and Va.
- Pb is the plane containing both hb and the line through points C and Vb.
- Pc is the plane containing both hc and the line through points C and Vc.
- The three vanishing points Va, Vb, Vc define a triangle, and the three altitudes ha, hb, hc intersect at the orthocenter of this triangle. For this special case, where the three direction vectors are mutually orthogonal, what is the significance of this point?
- If C is the optical center of the camera, show that the three angles ∠VaCVb, ∠VaCVc and ∠VbCVc are each equal to
- Use your results on vanishing points to draw a nice cartoon scene with a road or two, some houses and maybe a roadrunner and coyote.
- Suppose that a circle lies in a plane parallel to the image plane. Show that the perspective projection of the circle is a circle in the image plane and determine its radius.
-
Give an expression for the interaction matrix for two points p1 and p2 that satisfies
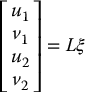
in which (u1, v1) and (u2, v2) are the image coordinates of the projection of p1 and p2, respectively, and ξ is the velocity of the moving camera.
- Show that the four vectors given in Equation (11.25) form a basis for the null space for the interaction matrix given in Equation (11.23).
- What is the dimension of the null space for the interaction matrix for two points? Give a basis for this null space.
-
Consider a stereo camera system attached to a robot manipulator. Derive the interaction matrix L that satisfies
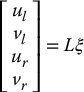
in which (ul, vl) and (ur, vr) are the image coordinates of the projection of p in the left and right images, respectively, and ξ is the velocity of the moving stereo camera system.
-
Consider a stereo camera system mounted to a fixed tripod observing the manipulator end effector. If the end effector velocity is given by ξ, derive the interaction matrix L that satisfies
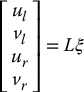
in which (ul, vl) and (ur, vr) are the image coordinates of the projection of p in the left and right images, respectively.
- Consider a fixed camera that observes the motion of a robot arm. Derive the interaction matrix that relates the velocity of the end effector frame to the image coordinates of the projection of the origin of the end effector frame.
-
Consider a camera mounted above a conveyor belt such that the optical axis is parallel to the world z-axis. The camera can translate and rotate about its optical axis, so in this case we have
 . Suppose the camera observes a planar object whose moments are given by
. Suppose the camera observes a planar object whose moments are given by
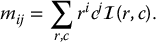
Derive the interaction matrix that satisfies
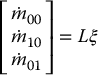
- Write a simulator for an image-based visual servo controller that uses the coordinates of four image points as features. Find initial and goal images for which the classical image-based control scheme will stop in a local minimum, that is, where the error lies in null space of the interaction matrix. Find initial and goal images for which the system diverges.
- Use the simulator you implemented for Problem 11–18 to demonstrate the robustness of image-based methods to errors in depth estimation.
- Use the simulator you implemented for Problem 11–18 to demonstrate the robustness of image-based methods to errors in the estimation of camera orientation. For example, use Euler angles to construct a rotation matrix that can be used to perturb the world coordinates of the four points used as features.
- It is often acceptable to use a fixed value of depth z = zd when constructing the interaction matrix. Here, zd denotes the depth when the camera is in its goal position. Use the simulator you implemented for Problem 11–18 to compare the performance of image-based control using the true value of depth vs. using the fixed value zd.
- Write a simulator for a partitioned controller that uses the coordinates of four image points as features. Find initial and goal images for which the controller fails. Compare the performance of this controller to the one you implemented for Problem 11–18.
Notes and References
Computer vision research dates back to the early sixties. In the early eighties several computer vision texts appeared. These books approached computer vision from the perspective of cognitive modeling of human vision [111], image processing [144], and applied robotic vision [66]. A comprehensive review of computer vision techniques through the early nineties can be found in [61], and an introductory treatment of methods in 3D vision can be found in [175]. Detailed treatments of the geometric aspects of computer vision can be found in [42] and [106]. A comprehensive review of the state of the art in computer vision at the turn of the century can be found in [47]. More recently, [26] has provided an updated treatment of robot vision, including feature detection and tracking, and vision-based control.
There are numerous design considerations when designing feature detectors and feature tracking algorithms. Should tracking be done directly in the image (using the position and orientation of the feature in the image as the state), or in the world frame (using the position and orientation of the camera as the state)? What should be the underlying tracking approach – a linearized approach such as the EKF, or a general nonlinear estimator? Which features are easiest to track? Which are most robust to variations in lighting? Which are most distinctive? These design considerations have led to a rich body of literature on the feature tracking problem in computer vision, and many general feature tracking algorithms have by now been made available in various open-source software libraries such as OpenCV [17] and Matlab’s Robotics and Computer Vision Toolboxes [26]. While the specifics of these algorithms may vary considerably, most can be seen as variations of the classical prediction-correction approach that lies at the heart of most state estimators. These issues are treated in standard computer vision texts (e.g., [47, 106, 26]).
Vision-based control of robotic systems dates back to the 1960’s and the robot known as Shakey that was built at SRI. However, the vision system for Shakey was much too slow for real-time control applications. Some of the earliest results of real-time, vision-based control were reported in [5] and [6], which described a robot that played ping pong.
The interaction matrix was first introduced in [146], where it was referred to as the feature sensitivity matrix. In [44] it was referred to as a Jacobian matrix, subsequently referred to in the literature as the image Jacobian, and in [39] it was given the name interaction matrix, the term we use in this text.
The performance problems associated with image-based methods were first rigorously investigated in [23]. This paper charted a course for the next several years of research in visual servo control.
The first partitioned method for visual servo was introduced in [107], which describes a system in which the three rotational degrees of freedom are controlled using position-based methods and the three translational degrees of freedom are controlled using image-based methods. Other partitioned methods have been reported in [33] and [116]. The method described in this chapter was reported in [27].
Motion perceptibility was introduced in [150] and [149]. The notion of resolvability, introduced in [124] and [125], is similar. In [43] the condition number of the interaction matrix is used for the purpose of feature selection.
Notes
- 1 The terminology eye-in-hand is standard within the visual servo community, even though the camera is typically attached to a link of the manipulator, and not directly to the end effector.
- 2 CMOS stands for complementary metal-oxide-semiconductor, a technology that has been widely adopted for use in integrated circuits.
- 3 Note that in our mathematical model, illustrated in Figure 11.1, we have placed the pinhole behind the image plane in order to simplify the model. Introductory texts on imaging often place the image plane behind the pinhole, resulting in an “upside-down” image. Our model provides an equivalent geometry, but eliminates the possible confusion of dealing with the “upside-down” image.
- 4 The line at infinity extends the real plane to include points at infinity in a manner analogous to adding + ∞ and − ∞ to the set of real numbers to obtain the extended real number system.
- 5 To avoid confusion with image coordinates u, v, in this chapter we use the symbol v to denote linear velocity.
- 6 When sd(t) is time-varying, it is necessary to design a trajectory tracking control law.