CHAPTER 7
PATH AND TRAJECTORY PLANNING
In previous chapters we studied the geometry of robot arms, developing solutions for both the forward and inverse kinematics problems. The solutions to these problems depend only on the intrinsic geometry of the robot, and they do not reflect any constraints imposed by the workspace in which the robot operates. In particular, they do not take into account the possibility of collision between the robot and objects in the workspace or collision between the robot and the boundaries of its workspace (e.g., walls, floor, closed doors). In this chapter we address the problem of planning collision-free paths for robots. We will assume that the initial and final configurations of the robot are specified and that the problem is to find a collision-free path connecting these configurations.
The description of this problem is deceptively simple, yet the path planning problem is among the most difficult problems in computer science. For example, the computation time required by the best known complete1 path planning algorithm grows exponentially with the number of internal degrees of freedom of the robot. For this reason, complete algorithms are used in practice only for simple robots with few degrees of freedom, such as mobile robots that translate in the plane. For robots that have more than a few degrees of freedom or are capable of rotational motion, path planning problems are often treated as search problems. The algorithms that are used for such problems are guided by heuristic strategies, and not guaranteed to find solutions for all problems. Nevertheless, they are quite effective in a wide range of practical applications, are fairly easy to implement, and require only moderate computation time for most problems.
Path planning provides a geometric description of robot motion, but it does not consider any dynamic aspects of the motion. For example, for a manipulator arm, what should be the joint velocities and accelerations while traversing the path? For a car-like robot, what should be the acceleration profile along the path? These kinds of questions are addressed by a trajectory planner. The trajectory planner computes a function q(t) that completely specifies the desired motion of the robot as it traverses the path.
We begin in Section 7.1 by revisiting the notion of configuration space that was first introduced in Chapter 1. We give a brief description of the geometry of the configuration space and describe how obstacles in the workspace can be mapped into the configuration space. Then, in Section 7.2, we consider the problem of planning the motion of polygon-shaped robots that translate in a planar workspace that contains polygonal objects. While this is a very special case, it has wide applicability to problems that involve mobile robots, such as the one shown in Figure 7.3. In Section 7.3 we present a first method that can be applied to general path planning problems, the so-called artificial potential field method. Potential field methods explore the configuration space by following the gradient of a function that rewards progress toward the goal while penalizing collision with objects in the workspace. It is generally not possible to construct such a function without introducing local minima, at which gradient descent algorithms will terminate without finding a solution. Randomization was introduced as a method to deal with this problem. In Section 7.4, we describe two methods that randomly generate a set of sample configurations, and use these as vertices in a graph that represents a set of free paths in the configuration space. Finally, since each of these methods generates a sequence of configurations, we describe how polynomial splines can be used to generate smooth trajectories from a sequence of configurations in Section 7.5.
7.1 The Configuration Space
In Chapter 3 we saw that the forward kinematic map can be used to determine the position and orientation of the end-effector frame given the vector of joint variables. Furthermore, the A matrices can be used to infer the position and orientation of any link of the robot. Since each link of the robot is assumed to be a rigid body, the A matrices can be used to infer the position of any point on the robot, given the values of the joint variables. Likewise, for a mobile robotic platform, if we rigidly attach a coordinate frame to the robot, we can infer the position of any point on the mobile platform once we know the position and orientation of the body-attached frame. In the path planning literature a complete specification of the location of every point on the robot is referred to as a configuration, and the set of all possible configurations is referred to as the configuration space. In this section, we formalize the notion of a configuration space, including how it can be represented mathematically, how the presence of objects in the workspace impose constraints on the set of valid configurations, and the representation of paths in the configuration space.
7.1.1 Representing the Configuration Space
We denote by 
a representation of the configuration space. For example, as we saw in Chapter 2, for any rigid object we can specify the location of every point on the object by rigidly attaching a coordinate frame to the object and then specifying the position and orientation of this frame. Thus, for a rigid object moving in the plane we could represent a configuration by the triple q = (x, y, θ), and the configuration space could be represented by 
. Alternatively, we could choose to represent the orientation of the object as a point on the unit circle, S1. In this case, the configuration space would be represented by 
.
For manipulator arms, the vector of joint variables often provides a convenient representation of a configuration. For a one-link revolute arm the configuration space is merely the set of orientations of the link, and thus 
, where S1 represents the unit circle. We can locally parameterize 
by a single parameter, the joint angle θ1, exactly as was done in Chapter 3 using the DH convention. For the two-link planar arm we have 
, in which T2 represents the torus, and we can represent a configuration by q = (θ1, θ2). For a Cartesian arm, we have 
and we can represent a configuration by q = (d1, d2, d3).
For mobile robots, we typically treat the robot as a single rigid object, ignoring the motion of individual components such as rotating wheels or propellers. For ground vehicles, the configuration space is typically represented as 
, or, in cases where the orientation of the vehicle is not relevant, as 
. The latter case is specifically addressed below, in Section 7.2. For robots that move in three-dimensional space, such as air vehicles or underwater robots, we typically define the configuration space as 
.
7.1.2 Configuration Space Obstacles
A collision occurs when any point on the robot contacts either an object in the workspace or the boundary of the workspace (e.g., walls or the floor), both of which are regarded as obstacles for the purposes of planning collision-free paths. Self-collision is also possible, for example if the end effector attached to a manipulator arm comes into contact with the base link, but we will not consider the case of self-collision here. To describe collisions we introduce some additional notation. We define the robot’s workspace as the Cartesian space in which the robot moves, denoted by 
. In general, we consider 
for mobile robots that move in the plane, and 
for robots that move in three-dimensional space (e.g., non-planar robot arms and mobile robots such as air vehicles). We denote the subset of the workspace that is occupied by the robot at configuration q by 
, and by 
the subset of the workspace occupied by the ith obstacle. To plan a collision free path we must ensure that the robot never reaches a configuration q that causes it to make contact with an obstacle. The set of configurations for which the robot collides with an obstacle is referred to as the configuration space obstacle and it is defined by
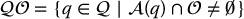
in which 
. The set of collision-free configurations, referred to as the free configuration space, is then simply the set difference
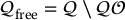
Example 7.1. (A Rigid Body that Translates in the Plane).
Consider a triangle-shaped mobile robot who possible motions include only translation in the plane as in Figure 7.1. For this case, the robot’s configuration space is 
, so it is particularly easy to visualize both the configuration space and the configuration space obstacle region.
If there is only one obstacle in the workspace and both the robot and the obstacle are convex polygons, it is a simple matter to compute the configuration space obstacle region 
. Let 
denote the vector that is normal to the ith edge of the robot and 
denote the vector that is normal to the ith edge of the obstacle. Define ai to be the vector from the origin of the robot’s coordinate frame to the ith vertex of the end effector, and bj to be the vector from the origin of the world coordinate frame to the jth vertex of the obstacle, as shown in Figure 7.1(a). The vertices of 
can be determined as follows.
- For each pair
and 
, if 
points between 
and 
, then add to 
the vertices bj − ai and bj − ai + 1. - For each pair
and 
, if 
points between 
and 
, then add to 
the vertices bj − ai and bj + 1 − ai.
This is illustrated in Figure 7.1(b). Note that this algorithm essentially places the robot at all positions where vertex-to-vertex contact between robot and obstacle are possible. The origin of the robot’s local coordinate frame at each such configuration defines a vertex of 
. The polygon defined by these vertices is 
.
If there are multiple convex obstacles 
, then the configuration space obstacle region is merely the union of the obstacle regions 
for the individual obstacles. For a nonconvex obstacle, the configuration space obstacle region can be computed by first decomposing the nonconvex obstacle into convex pieces 
computing the configuration space obstacle region 
for each piece, and finally, computing the union of the 
.
Example 7.2. (A Two-Link Planar Arm).
The computation of 
is more difficult for robots with revolute joints. Consider a two-link planar arm in a workspace containing a single obstacle as shown in Figure 7.2(a). The configuration space obstacle region is illustrated in Figure 7.2(b).
For values of θ1 very near π/2, the first link of the arm collides with the obstacle. When the first link is near the obstacle (θ1 near π/2), for some values of θ2 the second link of the arm collides with the obstacle. The region 
shown in Figure 7.2(b) was computed using a discrete grid on the configuration space. For each cell in the grid, a collision test was performed, and the cell was shaded when a collision occurred. This is only an approximate representation of 
; however, for robots with revolute joints, exact representations are very expensive to compute, and therefore such approximate representations are often used for robot arms with a few degrees of freedom.
Figure 7.1 (a) The robot is a triangle-shaped rigid object in a two-dimensional workspace that contains a single rectangular obstacle. (b) The boundary of the configuration space obstacle 
(shown as a dashed line) can be obtained by computing the convex hull of the configurations at which the robot makes vertex-to-vertex contact with the single convex obstacle.
Figure 7.2 (a) The robot is a two-link planar arm and the workspace contains a single, small polygonal obstacle. (b) The corresponding configuration space obstacle region contains all configurations q = (θ1, θ2) such that the arm at configuration q intersects the obstacle.
Computing 
for the two-dimensional case of 
and polygonal obstacles is straightforward, but, as can be seen from the two-link planar arm example, computing 
becomes difficult for even moderately complex configuration spaces. In the general case (for example, articulated arms or rigid bodies that can both translate and rotate), the problem of computing a representation of the configuration space obstacle region is intractable. One of the reasons for this complexity is that the size of the representation of the configuration space tends to grow exponentially with the number of degrees of freedom. This is easy to understand intuitively by considering the number of n-dimensional unit cubes needed to fill a space of size k. For the one-dimensional case k unit intervals will cover the space. For the two-dimensional case k2 squares are required. For the three-dimensional case k3 cubes are required, and so on. Therefore, in this chapter we will develop methods that avoid the construction of an explicit representation of 
or of 
.
7.1.3 Paths in the Configuration Space
The path planning problem is to find a path from an initial configuration 
to a final configuration 
, such that the robot does not collide with any obstacle as it traverses the path. More formally, a collision-free path from 
to 
is a continuous map, 
, with 
and 
. We will develop path planning methods that compute a sequence of discrete configurations (set points) in the configuration space. In Section 7.5 we will show how smooth trajectories can be generated from such a sequence of set points.
7.2 Path Planning for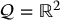 
Before considering the general path planning problem, we first consider the special case when 
, and in particular, situations in which both the robot and obstacles can be represented as polygons in the plane, and in which the robot can move in any arbitrary direction (e.g., there are no constraints on the directions of motion such as would exist for car-like mobile robots, which cannot move in the direction perpendicular to the car’s heading). Furthermore, we assume that the robot’s workspace, and thus also its configuration space, is bounded. This is often an acceptable approximation for situations in which mobile robots navigate in workspaces such as warehouses, factory floors, office buildings, etc.
In this case, as we have seen in Example 7.1, it is a simple matter to construct an explicit representation of the configuration space obstacle region (and thus, of the free configuration space). In this section, we present three algorithms that can be used to construct collision-paths, given as input an explicit, polygonal representation of the configuration space obstacle regions. All three algorithms build graph data structures to represent the set of possible paths, and thus, once these representations have been constructed, the path planning problem is reduced to a graph search problem, for which many algorithms exist.
A graph is defined as G = (V, E), in which V is a set of vertices, and E is a set of edges, each of which corresponds to a pair of vertices. An example is shown in Figure 7.3, in which the graph has vertices and edges
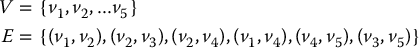
Vertices are said to be adjacent if they are connected by an edge. A path from vertex vi to vertex vj is a sequence of adjacent vertices, beginning at vi and ending at vj, or equivalently, the set of edges defined by the pairwise adjacent vertices in this path. For example, the edges (v1, v4), (v4, v2), (v2, v3), (v3, v5) define a path from v1 to v5.
Figure 7.3 A graph with five vertices and six edges.
7.2.1 The Visibility Graph
A visibility graph is a graph whose vertices can “see” each other, that is, edges in the graph correspond to paths that do not intersect the interior of any obstacle; the ‘line of sight” between adjacent vertices is unoccluded. For path planning in a polygonal configuration space, the set of vertices V includes (a) the start and goal configurations 
and 
, and (b) every vertex of the configuration space obstacles. The set of edges, E, includes all edges (vi, vj) such that the line segment joining vi to vj lies entirely in the free configuration space, or such that (vi, vj) corresponds to an edge of a polygonal configuration space obstacle. Figure 7.4(a) shows a configuration space containing polygonal obstacle regions, and Figure 7.4(b) shows the corresponding visibility graph.
Figure 7.4 This figure illustrates the construction of a free path using the visibility graph. (a) An environment that contains polygonal obstacles, with start and goal configurations 
and 
. (b) The visibility graph. (c) A semi-free path from 
to 
. (d) A free path from 
to 
, obtained by a small perturbation of the path vertices that contact obstacle vertices for the semi-free path.
Any path in the visibility graph corresponds to a semi-free path in the configuration space, where by semi-free we mean that the path lies in the closure of the free configuration space (i.e., either in the free configuration space, or in the boundary of the configuration space obstacle region). However, it is always possible to deform a semi-free path into a free path by a small perturbation of the semi-free path. As an example, Figure 7.4(c) shows a semi-free path from 
to 
(note that the path contacts the boundary of the configuration space obstacles at the obstacle vertices v2 and v6), and Figure 7.4(d) shows a corresponding free path.
It can be shown (Problem 7–7) that the visibility graph contains the shortest semi-free paths for any 
and 
, provided these 
and 
are included in the construction of the visibility graph. It should be noted that such shortest paths may not be desirable in practice, since they bring the robot arbitrarily near to obstacles in the workspace, which could easily lead to collision if there is any uncertainty in the robot’s location or in the map of the environment. For this reason, it is often preferable to plan paths that maximize the clearance between the robot and any obstacles. The so-called generalized Voronoi diagram, discussed next, can be used to construct such paths.
7.2.2 The Generalized Voronoi Diagram
Consider a set of discrete points in the plane, P = {p1, …, pn}. For each point pi, we define its Voronoi cell to be the set of points in the plane that are closer to pi than to any other pj ∈ P,
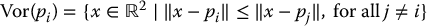
Two Voronoi regions are adjacent if Vor(pi)∩Vor(pj) ≠ ∅, in which case the intersection is a straight-line segment, referred to as a Voronoi edge, defined as
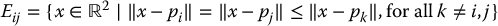
The Voronoi edge Eij comprises the set of points in the plane that are minimally equidistant to the points pi and pj.
If we consider the points pi as obstacles, then a collision-free path is merely a path that does not include any of the pi. Define the clearance of a path γ to be the minimum distance between the path and any point p ∈ P, i.e.,
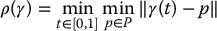
If 
and 
lie in Voronoi edges, then the maximum clearance path γ* connecting 
and 
is contained completely in the set of Voronoi edges.
All of these concepts can be generalized from the case of discrete points to the case of polygons in the plane. A polygon consists of a set of vertices that are connected by edges. Together, these vertices and edges are sometimes referred to as the features that define the polygon. Thus, a polygon feature f is either a vertex, v or an edge, e = (v, v′). Now, let P be the set of features corresponding to the polygonal configuration space obstacles. The distance from a point x to a feature f of a polygon is defined as
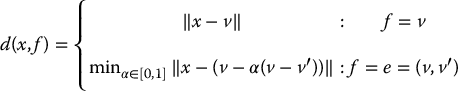
in which ‖x − v‖ is the Euclidean distance between the point x and the vertex v, and the expression min α ∈ [0, 1]‖x − (v − α(v − v′))‖ gives the minimum distance from the point x to the edge e = (v, v′).
We define the Voronoi cell of feature f to be the set of points in the plane that are closer to f than to any other feature f′ ∈ P,
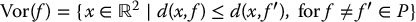
We can also generalize the concept of Voronoi edges to be the set of points minimally equidistant to two features,
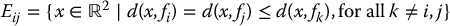
Since the set of features includes only points and line segments, the set of Voronoi edges will include only line segments that are minimally equidistant to two vertices or two edges, and sections of parabolas that are minimally equidistant to a vertex and an edge. We define the generalized Voronoi diagram as the graph G = (V, E) whose edges are these Voronoi edges, and whose vertices are points at which multiple Voronoi edges intersect.
For the case of polygonal obstacles, we define the clearance of a path γ to be the minimum distance between the path and any feature f ∈ P, i.e.,
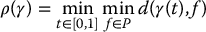
and, as above, if 
and 
lie in Voronoi edges, then the maximum clearance path γ* connecting 
and 
is contained completely in the set of Voronoi edges.
For the case when 
and 
do not lie in Voronoi edges, it is necessary to also construct collision-free paths from each of 
and 
to Voronoi edges. This is actually quite simple to do. If, for example, 
lies in the Voronoi region for a particular feature, f, a straight-line path from 
that follows the gradient 
will arrive to a Voronoi edge before reaching any other feature f′ (Problem 7–8). For the case of an edge feature, this gradient is given by
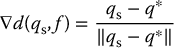
in which q* is the closest point in the edge to 
.
The path planning problem can now be solved as follows:
- Find the straight-line path from
to the nearest Voronoi edge. Let 
denote the point at which this path intersects the Voronoi edge. - Find the straight-line path from
to the nearest Voronoi edge. Let 
denote the point at which this path intersects the Voronoi edge. - Find a path in the generalized Voronoi diagram from
to 
.
Efficient algorithms exist for computing the exact generalized Voronoi diagram, but in practice numerical, grid-based algorithms are often used, since (a) they are much easier to implement (b) the error induced by resorting to a discrete grid is typically small relative to the clearance achieved by paths that lie in the generalized Voronoi diagram, and (c) grid-based representations are feasible for two-dimensional space. Figure 7.5 shows a polygonal configuration space and the corresponding generalized Voronoi diagram.
Figure 7.5 A polygonal configuration space containing five obstacles, and its generalized Voronoi diagram.
7.2.3 Trapezoidal Decompositions
The visibility graph and the generalized Voronoi diagram are both graphs whose edges correspond directly to paths in the configuration space. For the visibility graph, edges correspond to portions of specific semi-free paths, while for the generalized Voronoi diagram, each Voronoi edge corresponds to a portion of a specific free path. Neither of these representations explicitly captures any information about the geometry of the free configuration space.
In contrast, a spatial decomposition of the free configuration space is a collection of regions {R1, …, Rm} such that 
and int(Ri)∩int(Rj) = ∅ for all i ≠ j, where int(R) denotes the interior of region R. The regions Ri explicitly define the geometry of the free configuration space. A convex spatial decomposition has the additional property that each Ri is convex. Convex regions have the appealing property that for any qi, qj ∈ R, the line segment connecting them lies completely within R, that is, qi − α(qi − qj) ∈ R, for all α ∈ [0, 1]. Therefore, constructing a free path between two configurations in the same convex subset of 
is trivial. A trapezoidal decomposition is a special case from the class convex spatial decomposition that applies to the case of polygons in the plane.
Figure 7.6(a) shows trapezoidal decomposition for the free configuration space for the case of polygonal obstacles. Each region in the decomposition is a trapezoid consisting of polygon edges and vertical line segments incident upon vertices of the polygons2 A popular algorithm for constructing a trapezoidal decomposition proceeds by sweeping a vertical line across the configuration space, stopping at each vertex of the configuration space obstacle region, and making appropriate updates to the decomposition. Figure 7.6(b) shows one step in this process. At this stop of the sweep line, ℓ, regions R3 and R4 are “closed” and region R5 is “opened.”
Figure 7.6 A trapezoidal decomposition for the free configuration space for the case of polygonal obstacles.
The connectivity graph for a trapezoidal decomposition encodes adjacency relationships between the regions of the decomposition. The vertices of the connectivity graph correspond to the regions, and an edge exists between Ri and Rj if the two regions are adjacent (i.e., if Ri∩Rj ≠ ∅). Figure 7.6(c) shows the connectivity graph for the trapezoidal decomposition shown in Figure 7.6(a). For a given 
and 
, the path planning problem can be solved as follows.
- Determine the region Ri that contains the initial configuration
. - Determine the region Rj that contains the final configuration
. - Find a path in the connectivity graph from Ri to Rj.
- Construct a piecewise linear path from
and 
that passes successively through the cells found in Step 3, crossing from one region to the next at the midpoint of the boundary of the two regions.
7.3 Artificial Potential Fields
The methods described in Section 7.2 are applicable only for very simple configuration spaces. For more complex configuration spaces (e.g., SE(2) for a car-like robot, SE(3) for an air vehicle, or the n-torus for an n-link arm) it is typically not feasible to build an explicit representation of 
or of 
. An alternative is to develop a search algorithm that incrementally explores 
while searching for a path. One popular strategy for exploring 
uses an artificial potential field to guide the search.
The basic idea behind the potential field approach is to treat the robot as a point particle in the configuration space under the influence of an artificial potential field U. The field U is constructed so that the robot is attracted to the final configuration 
while being repelled from the boundaries of 
. If possible, U is constructed so that there is a single global minimum of U at 
and there are no local minima. Unfortunately, it is typically difficult or even impossible to construct such a field.
In most potential field path planners, the field U is constructed as an additive field consisting of one component that attracts the robot to 
and a second component that repels the robot from the boundary of 
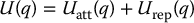
Given this formulation path planning can be treated as an optimization problem, namely the problem of finding the global minimum of U starting from initial configuration 
, and gradient descent methods are often used to find a solution. In physics, a conservative force field can be written as the negative gradient of a potential function. Thus, we may interpret gradient descent as being analogous to a particle moving under the influence of the force F = −∇U. Below we frequently refer to attractive and repulsive forces in order to exploit this natural intuition when defining potential fields.
We develop the potential field method for path planning in two stages. First, in Section 7.3.1, we develop the method for the special case of 
. By doing so, we can easily define U in terms of Euclidean distances, without dealing with the problem of defining metrics on arbitrary configuration spaces. This allows a straightforward initial development of the concepts and algorithms. In Section 7.3.2 we expand the approach to arbitrary configuration spaces. Rather than explicitly defining potential fields on these configuration spaces, we will define a collection of so-called workspace potential fields, and then show how the gradient of the corresponding configuration space potential can be computed using the Jacobian of the forward kinematic map. For both cases, we describe specific gradient descent algorithms for path planning.
7.3.1 Artificial Potential Fields for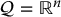 
For the case of 
, we will define an attractive potential in terms of the Euclidean distance to the goal, and a repulsive potential in terms of the Euclidean distance to the nearest obstacle boundary. We then describe how gradient descent methods can be used to find a collision-free path. Because gradient descent often fails for situations in which the potential field has multiple local minima, we end with a discussion of how randomization can be used to escape local minima of the potential function.
The Attractive Field
To attract the robot to its goal configuration, we will define an attractive potential field 
. At the goal configuration 
. There are several criteria that the potential field 
should satisfy. First, 
should be monotonically increasing with the distance to the goal configuration. The simplest choice for such a field grows linearly with this distance, a so-called conic well potential
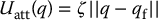
in which ζ is a parameter used to scale the effects of the attractive potential. The gradient of such a field has unit magnitude everywhere except the goal configuration, where it is zero. This can lead to stability problems since there is a discontinuity in the attractive force at the goal position.
The parabolic well potential given by
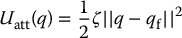
is continuously differentiable and increases monotonically with distance to the goal configuration. The attractive force is equal to the negative gradient of 
, which is given by (Problem 7–9)
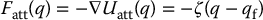
For the parabolic well the attractive force is a vector directed toward 
with magnitude linearly related to the distance to q from 
.
While this force converges linearly to zero as q approaches 
, which is a desirable property, it grows without bound as q moves away from 
. If 
is very far from 
, this may produce an initial attractive force that is very large. For this reason we may choose to combine the quadratic and conic potentials so that the conic potential is active when q is distant from 
, and the quadratic potential is active when q is near 
. Of course, it is necessary that the gradient be defined at the boundary between the conic and quadratic fields. Such a field can be defined by
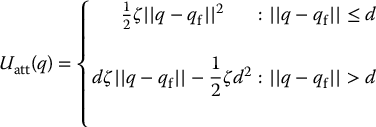
in which d is the distance that defines the transition from conic to parabolic well. In this case the force is given by
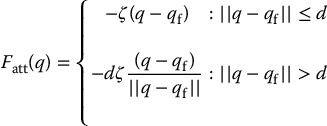
The gradient is well defined at the boundary of the two fields since at the boundary 
and the gradient of the quadratic potential is equal to the gradient of the conic potential 
.
The Repulsive Field
In order to prevent collisions between the robot and obstacles we will define a repulsive potential field that grows as the configuration approaches the boundary of 
. There are several criteria that such a repulsive field should satisfy. It should repel the robot from obstacles, never allowing the robot to collide with an obstacle, and, when the robot is far away from an obstacle, that obstacle should exert little or no influence on the motion of the robot. One way to achieve this is to define a potential function whose value approaches infinity as the configuration approaches an obstacle boundary, and whose value decreases to zero at a specified distance from the obstacle boundary.
We define ρ(q) to be the distance from configuration q to the boundary of 
,
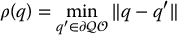
in which 
denotes the boundary of the configuration space obstacle region. We define ρ0 to be the distance of influence of an obstacle. This means that an obstacle will not repel the robot if the distance from q to the obstacle is greater than ρ0.
One potential function that meets the criteria described above is given by
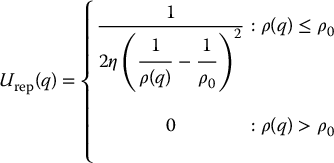
in which η is a parameter used to scale the effects of the attractive potential.
The repulsive force is equal to the negative gradient of 
. For ρ(q) ⩽ ρ0, this force is given by (Problem 7–13)
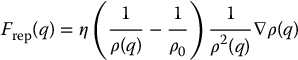
If 
is convex and b is the point on the boundary of 
that is closest to q, then ρ(q) = ||q − b||, and its gradient is
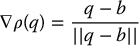
that is, the unit vector directed from b toward q.
If the obstacle is not convex, then the distance function ρ will not necessarily be differentiable everywhere, which implies discontinuity in the force vector. Figure 7.7 illustrates such a case. Here the obstacle region is defined by two rectangular obstacles. For all configurations to the left of the dashed line the force vector points to the right, while for all configurations to the right of the dashed line the force vector points to the left. Thus, when q crosses the dashed line, a discontinuity in force occurs. There are various ways to deal with this problem. The simplest of these is merely to ensure that the regions of influence of distinct obstacles do not overlap.
Figure 7.7 In this case the gradient of the repulsive potential given by Equation (7.2) is not continuous. In particular, the gradient changes discontinuously when q crosses the line midway between the two obstacles.
Gradient Descent Planning
Gradient descent is a well-known approach for solving optimization problems. The idea is simple. Starting at the initial configuration, take a small step in the direction of the negative gradient (which is the direction that decreases the potential as quickly as possible). This gives a new configuration, and the process is repeated until the final configuration is reached. More formally, a gradient descent algorithm constructs a sequence3 of configurations, q0, q1, …, qm such that 
and 
. The configuration at step i + 1 is given by
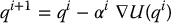
The scalar parameter αi scales the step size at the ith iteration. Some variations of gradient descent replace the gradient ∇U(qi) by a unit vector in the direction of the gradient; in this case αi completely determines the step size at the ith iteration. It is important that αi be small enough that the robot is not allowed to “jump into” obstacles while being large enough that the algorithm does not require excessive computation time. In motion planning problems the choice for αi is often made on an ad hoc or empirical basis, for example, based on the distance to the nearest obstacle or to the goal. A number of systematic methods for choosing αi can be found in the optimization literature.
It is unlikely that we will ever exactly satisfy the condition 
and for this reason gradient descent algorithms typically terminate when qi is sufficiently near the goal configuration 
, for example when 
, where we choose ε to be a sufficiently small constant, based on the task requirements.
Escaping Local Minima
The problem that plagues all gradient descent algorithms is the possible existence of local minima in the potential field. For appropriate choice of αi in (7.3), it can be shown that the gradient descent algorithm is guaranteed to converge to a minimum in the field, but there is no guarantee that this minimum will be the global minimum. In our case this implies that there is no guarantee that this method will find a path to 
. An simple example of this situation is shown in Figure 7.8.
Figure 7.8 The configuration qi is a local minimum in the potential field. At qi the attractive force exactly cancels the repulsive force and the planner fails to make further progress.
This problem has long been known in the optimization community, where probabilistic methods such as simulated annealing have been developed to cope with it. Similarly, randomized methods have been developed to deal with this and other problems in robot motion planning. One method for escaping local minima combines gradient descent with randomization. This approach uses gradient descent until the planner finds itself stuck in a local minimum, and then uses a random walk to escape the local minimum. This requires solving two problems: determining when the planner is stuck in a local minimum and defining the random walk.
Typically, a heuristic is used to recognize a local minimum. For example, if several successive qi lie within a small region of the configuration space, it is likely that there is a nearby local minimum. For example, if for some small positive εm we have ‖qi − qi + 1‖ < εm, ‖qi − qi + 2‖ < εm, and ‖qi − qi + 3‖ < εm then assume qi is near a local minimum, provided qi is not sufficiently near the goal configuration.
Defining the random walk requires a bit more care. One approach is to simulate Brownian motion. The random walk consists of t random steps. A random step from q = (q1, …, qn) is obtained by randomly adding a small fixed constant to each qi,
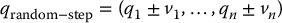
with vi a fixed small constant and the probability of adding + vi or − vi equal to 1/2 (that is, a uniform distribution). Without loss of generality, assume that q = 0. We can use probability theory to characterize the behavior of the random walk consisting of t random steps. In particular, if qt is the configuration reached after t random steps, the probability density function for qt = (q1, …, qn) is given by
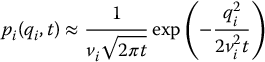
which is a zero mean Gaussian density function4 with variance v2it. This is a result of the central limit theorem, which states that the probability density function for the sum of k independent, identically distributed random variables tends to a Gaussian density function as k → ∞. The variance v2it essentially determines the range of the random walk. If certain characteristics of local minima (for example, the size of the basin of attraction) are known in advance, these can be used to select the parameters vi and t. Otherwise, they can be determined empirically or based on weak assumptions about the potential field.
7.3.2 Potential Fields for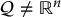 
For the case of 
, it is difficult to construct a potential field directly on the configuration space, and difficult to compute the gradient of such a field. The reasons for this include the difficulty of computing shortest distances to configuration space obstacles, the complex geometry of the configuration space itself, and the computational cost of computing an explicit representation of the boundary of the configuration space obstacle region. For this reason, when 
we will define workspace potential fields directly on the workspace of the robot, and then map the gradients of these fields to a corresponding gradient for a configuration space potential function.
In particular, for an n-link arm, we will define a potential field for each of the origins of the n DH frames (excluding the fixed, frame 0). These workspace potential fields will attract the origins of the DH frames to their goal locations while repelling them from obstacles. We will use these fields to define motions in the configuration space using the manipulator Jacobian matrix. A similar approach can be used for mobile robots. In this case, we define a set of control points on the robot that are sufficient to fully constrain its position, and define workspace potentials for each of these. For a mobile robot in the plane, two points are sufficient, while three (noncollinear) points are sufficient for free-flying robots.
The Attractive Field
To attract the robot to its goal configuration, we will define an attractive potential field 
for oi, the origin of the ith DH frame. When all n origins reach their goal positions, the arm will have reached its goal configuration. As above, choices include the conic well and parabolic well potentials.
If we denote the position of the origin of the ith DH frame by oi(q), then the conic well potential is given by
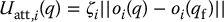
in which ζi is a parameter used to scale the effects of the attractive potential. The parabolic well potential is given by
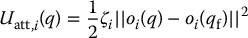
For the parabolic well, the workspace attractive force for oi is equal to the negative gradient of 
, which is given by
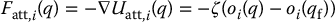
which is a vector directed toward 
with magnitude linearly related to the distance to oi(q) from 
.
We can combine the conic and parabolic well potentials as we did in Section 7.3.1, which yields
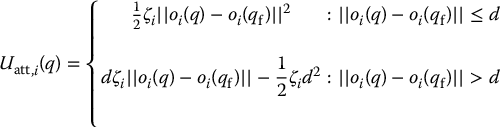
in which d is the distance that defines the transition from conic to parabolic well. In this case the workspace force for oi is given by
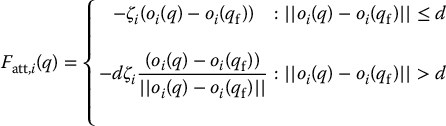
The gradient is well defined at the boundary of the two fields since at the boundary 
and the gradient of the quadratic potential is equal to the gradient of the conic potential 
.
Example 7.3. (Two-Link Planar Arm).
Consider the two-link planar arm shown in Figure 7.9 with a1 = a2 = 1 and with initial and final configurations given by
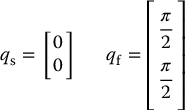
Using the forward kinematic equations for this arm (see Example 3.3.1) we obtain
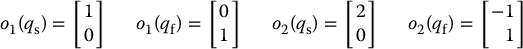
Using these coordinates for the origins of the two DH frames at their initial and goal configurations, assuming that d is sufficiently large, we obtain the attractive forces
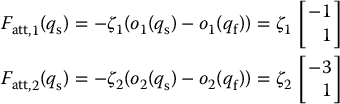
Figure 7.9 The initial configuration for the two-link arm is given by θ1 = θ2 = 0 and the final configuration is given by θ1 = θ2 = π/2. The origins for DH frames 1 and 2 are shown at both 
and 
.
The Repulsive Field
To prevent collisions, we will define a workspace repulsive potential field for the origin of each DH frame (excluding frame 0). Note that by defining repulsive potentials only for the origins of the DH frames we cannot ensure that collisions never occur (for example, the middle portion of a long link might collide with an obstacle), but it is fairly easy to modify the method to prevent such collisions as we will see below. For now, we will deal only with the origins of the DH frames.
We define ρ(oi(q)) to be the distance in the workspace from the origin of DH frame i to the nearest obstacle
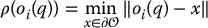
Likewise, we now define ρ0 to be the workspace distance of influence of an obstacle. This means that an obstacle will not repel oi if the distance from oi to the obstacle is greater than ρ0.
Our workspace repulsive potential is now given by
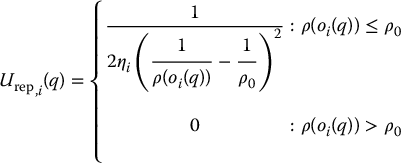
The workspace repulsive force is equal to the negative gradient of 
. For ρ(oi(q)) ⩽ ρ0, this force is given by
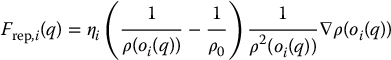
in which the notation ∇ρ(oi(q)) indicates the gradient ∇ρ(x) evaluated at x = oi(q). If the obstacle region is convex and b is the point on the obstacle boundary that is closest to oi, then ρ(oi(q)) = ||oi(q) − b||, and its gradient is
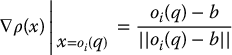
that is, the unit vector directed from b toward oi(q).
Example 7.4. (Two-Link Planar Arm).
Consider Example 7.3, with a single convex obstacle in the workspace as shown in Figure 7.10. Let ρ0 = 1. This prevents the obstacle from repelling o1, which is reasonable since link 1 can never contact the obstacle. The nearest obstacle point to o2 is the vertex b of the polygonal obstacle. Suppose that b has the coordinates (2, 0.5). Then the distance from 
to b is 
and 
. The repulsive force at the initial configuration for o2 is then given by
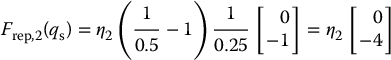
This force has no effect on joint 1, but causes joint 2 to rotate slightly in the clockwise direction, moving link 2 away from the obstacle.
Figure 7.10 The obstacle shown repels o2, but is outside the distance of influence for o1. Therefore, it exerts no repulsive force on o1.
As mentioned above, defining repulsive fields only for the origins of the DH frames does not guarantee that the robot cannot collide with an obstacle. Figure 7.11 shows an example where this is the case. In this figure o1 and o2 are very far from the obstacle and therefore the repulsive influence may not be great enough to prevent link 2 from colliding with the obstacle. To cope with this problem we can use a set of floating repulsive control points ofloat, i typically one per link. The floating control points are defined as points on the boundary of a link that are closest to any workspace obstacle. Obviously the choice of the ofloat, i depends on the configuration q. For the case shown in Figure 7.11, ofloat, 2 would be located near the center of link 2, thus repelling the robot from the obstacle. The repulsive force acting on ofloat, i is defined in the same way as for the other control points using Equation (7.5).
Figure 7.11 The repulsive forces exerted on the origins of the DH frames o1 and o2 may not be sufficient to prevent a collision between link 2 and the obstacle.
Mapping Workspace Forces to Joint Torques
We have shown how to construct potential fields in the robot’s workspace that induce artificial forces on the origins oi of the DH frames for the robot arm. In this section we describe how these artificial forces can be mapped to artificial joint torques.
As we derived in Chapter 4 using the principle of virtual work, if τ denotes the vector of joint torques induced by the workspace force F exerted at the end effector, then
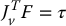
where Jv includes the top three rows of the manipulator Jacobian. We do not use the lower three rows, since we have considered only attractive and repulsive workspace forces, and not attractive and repulsive workspace torques. Note that for each oi an appropriate Jacobian must be constructed, but this is straightforward given the techniques described in Chapter 4 and the A matrices for the arm. We denote the Jacobian for oi by 
.
Example 7.5. (Two-Link Planar Arm).
Consider again the two-link arm of Example 7.3 with repulsive workspace forces as given in Example 7.4. The Jacobians that map joint velocities to linear velocities satisfy
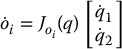
For the two-link arm the Jacobian matrix for o2 is merely the Jacobian that we derived in Chapter 4, namely
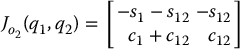
The Jacobian matrix for o1 is similar, but takes into account that motion of joint 2 does not affect the velocity of o1. Thus
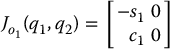
At 
we have
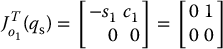
and
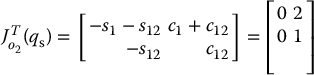
Using these Jacobians, we can easily map the workspace attractive and repulsive forces to joint torques. If we let ζ1 = ζ2 = η2 = 1 we obtain
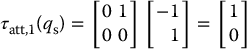
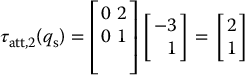
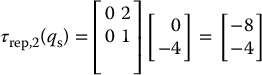
The total artificial joint torque acting on the arm is the sum of the artificial joint torques that result from all attractive and repulsive potentials
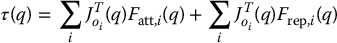
It is essential that we add the joint torques and not the workspace forces. In other words, we must use the Jacobians to transform forces to joint torques before we combine the effects of the potential fields. For example, Figure 7.12 shows a case in which two workspace forces F1 and F2, act on opposite corners of a rectangle. It is easy to see that F1 + F2 = 0, but that the combination of these forces produces a pure torque about the center of the rectangle.
Example 7.6. (Two-Link Planar Arm).
Consider again the two-link planar arm of Example 7.3, with joint torques as determined in Example 7.5. In this case the total joint torque induced by the attractive and repulsive workspace potential fields is given by
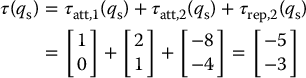
These joint torques have the effect of causing each joint to rotate in a clockwise direction, away from the goal, due to the close proximity of o2 to the obstacle. By choosing a smaller value for η2, this effect can be overcome.
Figure 7.12 The two forces illustrated in the figure are vectors of equal magnitude in opposite directions. Vector addition of these two forces produces zero net force, but there is a net torque induced by these forces.
Application to Mobile Robots
The methods described in this section can easily be extended to the case of mobile robots. To do so, we define a set of control points on the robot {oi}i = 1…m such that 
when 
for i = 1, …m. We then proceed as above, treating these oi in the same way that we treated DH frames. The Jacobian matrix used in this case is given by
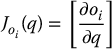
and an appropriate gradient for the configuration space potential function is given by
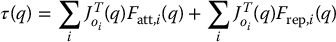
in which τ includes forces and moments applied with respect to the body-attached coordinate frame of the robot.
Example 7.7. (A Polygonal Robot in the Plane).
Consider the polygonal robot shown in Figure 7.13. The vertex a has coordinates (ax, ay) in the robot’s local coordinate frame. Therefore, if the robot’s configuration is given by q = (x, y, θ), the forward kinematic map for vertex a (that is, the mapping from q = (x, y, θ) to the global coordinates of the vertex a) is given by
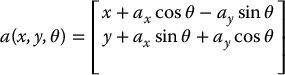
The corresponding Jacobian matrix is given by
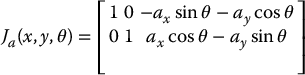
Using the transpose of the Jacobian to map the workspace forces to generalized forces, we obtain
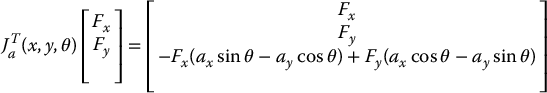
The bottom entry in this vector corresponds to the torque exerted about the origin of the robot frame.
Figure 7.13 In this example, the robot is a polygon whose configuration can be represented as q = (x, y, θ), in which θ is the angle from the world x-axis to the x-axis of the robot’s local frame. A force F is exerted on vertex a with local coordinates (ax, ay).
Gradient Descent Planning
As above, the gradient descent algorithm constructs a sequence of configurations, q0, q1, …, qm such that 
and 
, but in this case the kth iteration is given by
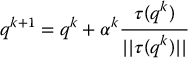
in which τ is given by (7.6). The scalar αk determines the step size at the kth iteration, and the algorithm terminates when 
, where we choose ε to be a sufficiently small constant, based on the task requirements.
The problem of local minima in the potential field also exists for this approach to defining workspace potentials and mapping workspace gradients to the configuration space. An example of this situation is shown in Figure 7.14.
Figure 7.14 The configuration qmin is a local minimum in the potential field. At qmin the attractive force exactly cancels the repulsive force and the planner fails to make further progress.
There are a number of design choices that must be made when using this approach.
- The constant ζi in Equation (7.4) controls the relative influence of the attractive potential for control point oi. It is not necessary that all of the ζi be set to the same value. Typically we assign a larger weight to one of the oi than to the others, producing a “follow the leader” type of motion, in which the leader oi is quickly attracted to its final position and the robot then reorients itself so that the other oi reach their final positions.
- The constant ηi in Equation (7.5) controls the relative influence of the repulsive potential for oi. As with the ζi it is not necessary that all of the ηi be set to the same value. In particular, we typically set the value of ηi to be much smaller for obstacles that are near the goal position of the robot (to avoid having these obstacles repel the robot from the goal).
- The constant ρ0 in Equation (7.5) defines the distance of influence for obstacles. As with the ηi we can define a distinct value of ρ0 for each obstacle. In particular, we do not want any obstacle’s region of influence to include the goal position of any repulsive control point. We may also wish to assign distinct values of ρ0 to the obstacles to avoid the possibility of overlapping regions of influence for distinct obstacles.
7.4 Sampling-Based Methods
The potential field approaches described above incrementally explore 
by generating a sequence of configurations q0, …, qm using a gradient descent approach. This exploration is inherently goal-driven (due to the attractive potential), and it is this bias that makes the approach susceptible to failure due to the presence of local minima in the potential field. As we have seen, applying a random walk can be an effective way to escape local minima, abandoning temporarily the goal-driven behavior in favor of a randomized strategy. Taken to an extreme, we could design a planner that completely abandons goal-driven search, instead relying completely on randomized strategies. This is the approach taken by sampling-based planners5.
Sampling-based planners generate a sequence of configurations using a random sampling strategy. The simplest such strategy is merely to generate random samples from a uniform probability distribution on the configuration space. If two samples are sufficiently near to one another, planning a path between them can be accomplished using a simple, local planner. Iteratively applying this strategy produces a graph G = (V, E) in which the vertex set V includes the randomly generated sample configurations, and edges correspond to local paths between sample configurations that lie in close proximity to one another. The graph G is referred to as a configuration space roadmap.
In this section, we will describe two sampling-based planning algorithms. The first algorithm builds a probabilistic roadmap or PRM, which is a roadmap that attempts to uniformly cover the entire free configuration space. This approach is particularly useful when many planning problems are to be solved for a single workspace, so that the cost of building the roadmap can be amortized over many planning instances. The second algorithm builds a rapidly-exploring random Tree or RRT, which is a random tree whose root vertex corresponds to the initial configuration 
. By using a clever sampling strategy to generate new vertices in the tree, this method is able to rapidly explore the free configuration space, and has proven to be effective for solving even difficult path planning problems.
7.4.1 Probabilistic Roadmaps (PRM)
In general, a configuration space roadmap is a one-dimensional network of curves that effectively represents 
. A roadmap is typically represented as a graph, in which edges correspond to curve segments, whose intersections correspond to vertices. When using roadmap methods, planning comprises three stages: (1) find a path from 
to a configuration qa in the roadmap, (2) find a path from 
to a configuration qb in the roadmap, (3) find a path in the roadmap from qa to qb. Steps (1) and (2) are typically much easier than finding a path from 
to 
. The visibility graph and generalized Voronoi diagram described in Section 7.2 are both examples of configuration space roadmaps (although for the visibility graph, both 
and 
are included in the roadmap by construction).
A probabilistic roadmap, or PRM, is a configuration space roadmap whose vertices correspond to randomly generated configurations, and whose edges correspond to collision-free paths between configurations. Constructing a PRM is a conceptually straightforward process. First, a set of random configurations is generated to serve as the vertices in the roadmap. Then, a simple, local path planner is used to generate paths that connect pairs of configurations. Finally, if the initial roadmap consists of multiple connected components6, it is augmented during an enhancement phase, in which new vertices and edges are added in an attempt to connect disjoint components of the roadmap. To solve a path planning problem, the simple, local planner is used to add 
and 
to the roadmap, and the resulting roadmap is searched for a path from 
to 
. These four steps are illustrated in Figure 7.15. We now discuss these steps in more detail.
Figure 7.15 This figures illustrates the steps in the construction of a probabilistic roadmap for a two-dimensional configuration space containing polygonal obstacles. (a) First, a set of random samples is generated in the configuration space. Only collision-free samples are retained. (b) Each sample is connected to its nearest neighbors using a simple, straight-line path. If such a path causes a collision, the corresponding samples are not connected in the roadmap. (c) Since the initial roadmap contains multiple connected components, additional samples are generated and connected to the roadmap in an enhancement phase. (d) A path from 
to 
is found by connecting 
and 
to the roadmap and then searching this augmented roadmap for a path from 
to 
.
Sampling the Configuration Space
The simplest way to generate sample configurations is with uniform random sampling of the configuration space. Sample configurations that lie in 
are discarded. A simple collision checking algorithm can determine when this is the case. The disadvantage of this approach is that the number of samples it places in any particular region of 
is proportional to the volume of the region. Therefore, uniform sampling is unlikely to place samples in narrow passages of 
. In the PRM literature, this is referred to as the narrow passage problem. It can be dealt with either by using more intelligent sampling schemes, or by using an enhancement phase during the construction of the PRM. In this section, we discuss the latter option.
Connecting Pairs of Configurations
Given a set of vertices that correspond to configurations, the next step in building the PRM is to determine which pairs of vertices should be connected by the local path planner. The typical approach is to attempt to connect each vertex to its k nearest neighbors, with k a parameter chosen by the user. Of course, to define the nearest neighbors, a distance function is required. Table 7.1 lists four distance functions that have been popular in the PRM literature. In this table, q and q′ are the two configurations corresponding to different vertices in the roadmap, qi refers to the value of the ith coordinate of q, 
is a set of reference points on the robot, and p(q) refers to the workspace coordinates of reference point p at configuration q. Of these, the simplest, and perhaps most commonly used, is the 2-norm in configuration space.
Table 7.1 Four commonly used distance functions.
2-norm in  :
|
|
∞-norm in  :
|
max n|q′i − qi| |
| 2-norm in workspace: | 
|
| ∞-norm in workspace: | 
|
Once pairs of neighboring vertices have been identified, a simple local planner is used to connect them. Often, a straight line in configuration space is used as the candidate plan, and thus, planning the path between two vertices is reduced to collision checking along a straight-line path in the configuration space. If a collision occurs on this path, it can be discarded, or a more sophisticated planner can be used to attempt to connect the vertices.
The simplest approach to collision detection along the straight-line path is to sample the path at a sufficiently fine discretization, and to check each sample for collision. This method works, provided the discretization is fine enough, but it is very inefficient. This is because many of the computations required to check for collision at one sample are repeated for the next sample (assuming that the robot has moved only a small amount between the two configurations). For this reason, incremental collision detection approaches have been developed. While these approaches are beyond the scope of this text, a number of collision detection software packages are available in the public domain. Most developers of robot motion planners use one of these packages, rather than implementing their own collision detection routines.
Enhancement
After the initial PRM has been constructed, it is likely that it will consist of multiple connected components. Often these individual components lie in large regions of 
that are connected by narrow passages in 
. The goal of the enhancement process is to connect as many of these disjoint components as possible.
One approach to enhancement is merely to attempt to connect pairs of vertices in two disjoint components, perhaps by using a more sophisticated planner such as described in Section 7.3. A common approach is to identify the largest connected component, and to attempt to connect the smaller components to it. The vertex in the smaller component that is closest to the larger component is typically chosen as the candidate for connection. A second approach is to choose a vertex randomly as a candidate for connection, and to bias the random choice based on the number of neighbors of the vertex; a vertex with fewer neighbors in the roadmap is more likely to be near a narrow passage, and should be a more likely candidate for connection.
Another approach to enhancement is to add more random vertices to the roadmap, in the hope of finding vertices that lie in or near the narrow passages. One approach is to identify vertices that have few neighbors, and to generate sample configurations in regions around these vertices. The local planner is then used to attempt to connect these new configurations to the roadmap.
Path Smoothing
After the PRM has been generated, path planning amounts to connecting 
and 
to the roadmap using the local planner, and then performing path smoothing, since the resulting path will be composed of straight-line segments in the configuration space. The simplest path smoothing algorithm is to select two random points on the path and try to connect them with the local planner. This process is repeated until no significant progress is made.
7.4.2 Rapidly-Exploring Random Trees (RRTs)
In the classical PRM algorithm, the ith sample configuration is obtained by sampling from a uniform probability distribution on 
, independent of any previously generated samples7. As a result, it is possible, and even likely, that at any given iteration the newly generated sample configuration may be quite far from any existing vertices in the current roadmap. In such cases, the local planner is likely to fail to connect the new sample to any existing vertex, increasing the number of connected components in the roadmap. An alternative approach is to grow a single tree, starting from a vertex that corresponds to 
, until some leaf vertex reaches the goal configuration. This is the approach embodied by rapidly-exploring random trees (RRTs).
The construction of an RRT is an iterative process in which a new vertex is added to an existing tree at each iteration. The process of adding a new vertex begins by generating a random sample, qsample, from a uniform probability distribution on 
; however, unlike the construction of PRMs, this vertex is not added to the existing tree. Instead, qsample is used to determine how to “grow” the current tree. This is done by choosing the vertex qnear in the existing tree that is closest to qsample, and taking a small step from qnear in the direction of qsample. The configuration at which this step arrives, qnew, is added to the tree, and an edge is added from qnear to qnew. Figure 7.16 illustrates the process for a single iteration of the RRT construction algorithm.
Figure 7.16 A new vertex is added to an existing tree by (i) generating a sample configuration generate qsample from a uniform probability distribution on 
, (ii) identifying qnear, the vertex in the current tree that is nearest to qsample, and (iii) taking a small step from qnear toward qsample.
While RRT-based algorithms have proven to be very effective in planning collision-free paths for robots, their true power lies in the method by which the new node qnew is generated and connected to the existing tree. For PRMs, a new node is connected to the tree by solving a local path planning problem. For RRTs, the configuration qnew is chosen by “taking a step” toward qsample. The simplest way to achieve this, of course, is to step along a straight-line path toward qsample, but more general methods can be applied. Consider, for example, a robot whose system dynamics are described by
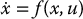
in which x denotes the state of the system and u denotes an input. If we define our RRT on the state space instead of the configuration space, we can generate the vertex xnew by integrating the dynamics (7.7) forward in time from the initial condition given by xnear
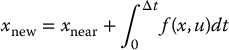
Evaluating this integral requires knowing an appropriate control input u. Choosing u to ensure that xnew lies along the line connecting xnear to xsample is a difficult problem, but luckily, ensuring that xnew lies exactly on this line is not essential to the efficacy of RRT algorithms. A popular way to determine xnew is to randomly select a set of candidate inputs, ui, evaluate (7.8) for each of these, and retain the result that makes the best progress toward xsample. Using this approach, RRTs have been applied to motion planning problems for car-like robots, unmanned air vehicles, autonomous underwater vehicles, spacecraft, satellites, and many others.
7.5 Trajectory Planning
In Section 7.1.3, we defined a path8 from q0 to 
in configuration space as a continuous map, 
, with γ(0) = q0 and 
. A trajectory is a function of time q(t) such that q(t0) = q0 and 
. In this case, tf − t0 represents the amount of time taken to execute the trajectory. Since the trajectory is parameterized by time, we can compute velocities and accelerations along the trajectories by differentiation. If we think of the argument to γ as a time variable, then a path is a special case of a trajectory, one that will be executed in one unit of time. In other words, in this case γ gives a complete specification of the robot’s trajectory, including the time derivatives (since one need only differentiate γ to obtain these).
As seen above, a path planning algorithm will not typically give the map γ; it will give only a sequence of points (called via points) along the path. This is also the case for other ways in which a path could be specified. In some cases, paths are specified by giving a sequence of end-effector poses, 
. In this case, the inverse kinematic solution must be used to convert this to a sequence of joint configurations. A common way to specify paths for industrial robots is to physically lead the robot through the desired motion with a teach pendant, the so-called teach and playback mode. In some cases, this may be more efficient than deploying a path planning system, for example, in static environments when the same path will be executed many times. In this case, there is no need for calculation of the inverse kinematics; the desired motion is simply recorded as a set of joint angles (actually as a set of encoder values).
Below, we first consider point-to-point motion. In this case the task is to plan a trajectory from an initial configuration q(t0) to a final configuration q(tf). In some cases, there may be constraints on the trajectory (for example, if the robot must start and end with zero velocity). Nevertheless, it is easy to realize that there are infinitely many trajectories that will satisfy a finite number of constraints on the endpoints. It is common practice therefore to choose trajectories from a finitely parameterizable family, for example, polynomials of degree n, where n depends on the number of constraints to be satisfied. This is the approach that we will take in this text. Once we have seen how to construct trajectories between two configurations, it is straightforward to generalize the method to the case of trajectories specified by multiple via points.
7.5.1 Trajectories for Point-to-Point Motion
As described above, the problem is to find a trajectory that connects the initial and final configurations while satisfying other specified constraints at the endpoints, such as velocity and/or acceleration constraints. Without loss of generality, we will consider planning the trajectory for a single joint, since the trajectories for the remaining joints will be created independently and in exactly the same way. Thus, we will concern ourselves with the problem of determining q(t), where q(t) is a scalar joint variable.
We suppose that at time t0 the joint variable satisfies
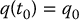
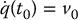
and we wish to attain the values at tf
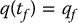
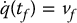
Figure 7.17 shows a suitable trajectory for this motion. In addition, we may wish to specify the constraints on initial and final accelerations. In this case we have two additional equations
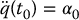
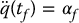
Figure 7.17 A typical joint space trajectory.
Below we will investigate several specific ways to compute trajectories using low-order polynomials. We begin with cubic polynomials, which allow specification of initial and final positions and velocities. We then describe quintic polynomial trajectories, which also allow the specification of the initial and final accelerations. After describing these two general polynomial trajectories, we describe trajectories that are pieced together from segments of constant acceleration.
Cubic Polynomial Trajectories
Consider first the case where we wish to generate a polynomial joint trajectory between two configurations, and that we wish to specify the start and end velocities for the trajectory. This gives four constraints that the trajectory must satisfy. Therefore, at a minimum we require a polynomial with four independent coefficients that can be chosen to satisfy these constraints. Thus, we consider a cubic trajectory of the form
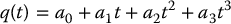
Then the desired velocity is given as
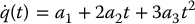
Combining Equations (7.15) and (7.16) with the four constraints yields four equations in four unknowns
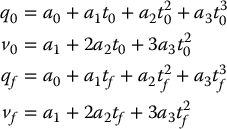
These four equations can be combined into a single matrix equation
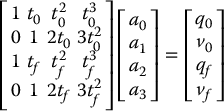
It can be shown (Problem 7–19) that the determinant of the coefficient matrix in Equation (7.17) is equal to (tf − t0)4 and, hence, Equation (7.17) always has a unique solution provided a nonzero time interval is allowed for the execution of the trajectory.
Example 7.8. (Cubic Polynomial Trajectory).
As an illustrative example, we may consider the special case that the initial and final velocities are zero. Suppose we take t0 = 0 and tf = 1 sec, with
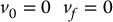
Thus, we want to move from the initial position q0 to the final position qf in 1 second, starting and ending with zero velocity. From Equation (7.17) we obtain
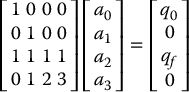
This is then equivalent to the four equations
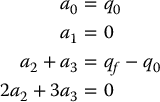
These latter two equations can be solved to yield
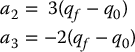
The required cubic polynomial function is therefore
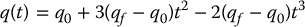
The corresponding velocity and acceleration curves are given as
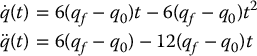
Figure 7.18 shows these trajectories with q0 = 10°, qf = −20°.
Figure 7.18 (a) Cubic polynomial trajectory. (b) Velocity profile for cubic polynomial trajectory. (c) Acceleration profile for cubic polynomial trajectory.
Quintic Polynomial Trajectories
As can be seen in Figure 7.18, a cubic trajectory gives continuous positions and velocities at the start and finish points times but discontinuities in the acceleration. The derivative of acceleration is called the jerk. A discontinuity in acceleration leads to an impulsive jerk, which may excite vibrational modes in the manipulator and reduce tracking accuracy. For this reason, one may wish to specify constraints on the acceleration as well as on the position and velocity. In this case, we have six constraints (one each for initial and final configurations, initial and final velocities, and initial and final accelerations). Therefore we require a fifth order polynomial
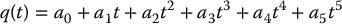
Using Equations (7.9)–(7.14) and taking the appropriate number of derivatives we obtain the following equations,
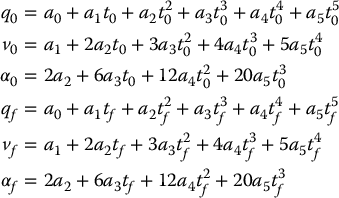
which can be written as
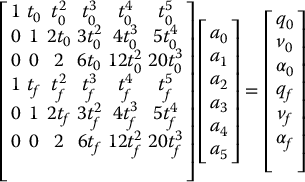
Example 7.9. (Quintic Polynomial Trajectory).
Figure 7.19 shows a quintic polynomial trajectory with q(0) = 0, q(2) = 20 with zero initial and final velocities and accelerations.
Figure 7.19 (a) Quintic polynomial trajectory, (b) its velocity profile, and (c) its acceleration profile.
Linear Segments with Parabolic Blends (LSPB)
Another way to generate suitable joint space trajectories is by using so-called linear segments with parabolic blends (LSPB). This type of trajectory has a trapezoidal velocity profile and is appropriate when a constant velocity is desired along a portion of the path. The LSPB trajectory is such that the velocity is initially “ramped up” to its desired value and then “ramped down” when it approaches the goal position. To achieve this we specify the desired trajectory in three parts. The first part from time t0 to time tb is a quadratic polynomial. This results in a linear “ramp” velocity. At time tb, called the blend time, the trajectory switches to a linear function. This corresponds to a constant velocity. Finally, at tf − tb the trajectory switches once again, this time to a quadratic polynomial so that the velocity is linear.
We choose the blend time tb so that the position curve is symmetric as shown in Figure 7.20. For convenience suppose that t0 = 0 and 
. Then between times 0 and tb we have
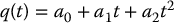
so that the velocity is
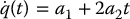
The constraints q0 = 0 and 
imply that
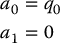
At time tb we want the velocity to equal a given constant, say V. Thus, we have
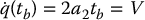
which implies that
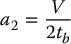
Therefore the required trajectory between 0 and tb is given as
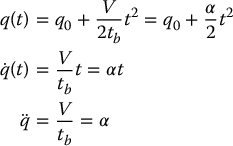
where α denotes the acceleration.
Figure 7.20 Blend times for LSPB trajectory.
Now, between time tb and tf − tb, the trajectory is a linear segment with velocity V
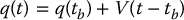
Since, by symmetry,
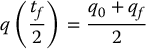
we have
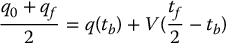
which implies that
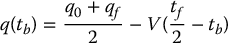
Since the two segments must “blend” at time tb, we require
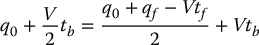
which, upon solving for the blend time tb, gives
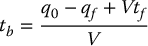
Note that we have the constraint 
. This leads to the inequality
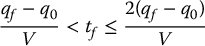
To put it another way we have the inequality
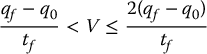
Thus, the specified velocity must be between these limits or the motion is not possible.
The portion of the trajectory between tf − tb and tf is now found by symmetry considerations (Problem 7–23). The complete LSPB trajectory is given by
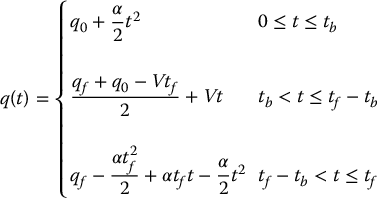
Figure 7.21(a) shows such an LSPB trajectory, where the maximum velocity V = 60. In this case 
. The velocity and acceleration curves are given in Figures 7.21(b) and 7.21(c), respectively.
Figure 7.21 (a) LSPB trajectory. (b) Velocity profile for LSPB trajectory. (c) Acceleration profile for LSPB trajectory.
Minimum-Time Trajectories
An important variation of the LSPB trajectory is obtained by leaving the final time tf unspecified and seeking the “fastest” trajectory between q0 and qf with a given constant acceleration α, that is, the trajectory with the final time tf a minimum. This is sometimes called a bang-bang trajectory since the optimal solution is achieved with the acceleration at its maximum value + α until an appropriate switching time ts at which time it abruptly switches to its minimum value − α (maximum deceleration) from ts to tf.
Returning to our simple example in which we assume that the trajectory begins and ends at rest, that is, with zero initial and final velocities, symmetry considerations would suggest that the switching time ts is just 
. This is indeed the case. For nonzero initial and/or final velocities, the situation is more complicated and we will not discuss it here. If we let Vs denote the velocity at time ts then we have Vs = αts and using Equation (7.20) with tb = ts we obtain
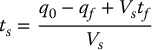
The symmetry condition 
implies that
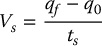
and using the fact that Vs = αts, we obtain
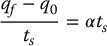
which implies that
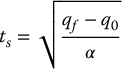
Figure 7.22 shows the position, velocity, and acceleration for such a minimum-time trajectory.
Figure 7.22 (a) Minimum-time trajectory. (b) Velocity profile for minimum-time trajectory. (c) Acceleration profile for minimum-time trajectory.
7.5.2 Trajectories for Paths Specified by Via Points
Now that we have examined the problem of planning a trajectory between two configurations, we generalize our approach to the case of planning a trajectory that passes through a sequence of configurations, called via points. Consider the simple example of a path specified by three points, q0, q1, and q2, such that the via points are reached at times t0, t1, and t2, respectively. If in addition to these three constraints we impose constraints on the initial and final velocities and accelerations, we obtain the following set of constraints,
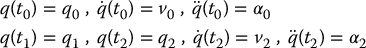
which could be satisfied by generating a trajectory using the sixth-order polynomial
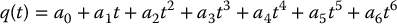
One advantage to this approach is that, since q(t) is continuously differentiable, we need not worry about discontinuities in either velocity or acceleration at the via point, q1. However, to determine the coefficients for this polynomial, we must solve a linear system of dimension seven. The clear disadvantage to this approach is that as the number of via points increases, the dimension of the corresponding linear system also increases, making the method intractable when many via points are used.
An alternative to using a single high-order polynomial for the entire trajectory is to use low-order polynomials for trajectory segments between adjacent via points. These polynomials are sometimes referred to as interpolating polynomials or blending polynomials. With this approach, we must take care that velocity and acceleration constraints are satisfied at the via points, where we switch from one polynomial to another.
For the first segment of the trajectory, suppose that the initial and final times are t0 and tf, respectively, and the constraints on initial and final velocities are given by
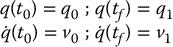
the required cubic polynomial for this segment of the trajectory can be computed from
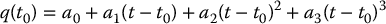
where
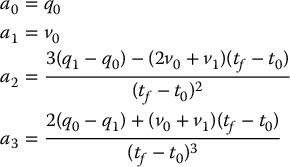
A sequence of moves can be planned using the above formula by using the end conditions qf, vf of the ith move as initial conditions for the subsequent move.
Figure 7.23 shows a 6-second move, computed in three parts using Equation (7.24), where the trajectory begins at 10° and is required to reach 40° at 2 seconds, 30° at 4 seconds, and 90° at 6 seconds, with zero velocity at 0, 2, 4, and 6 seconds.
Figure 7.23 (a) Cubic spline trajectory made from three cubic polynomials. (b) Velocity profile for multiple cubic polynomial trajectory. (c) Acceleration profile for multiple cubic polynomial trajectory.
Figure 7.24 shows the same 6-second trajectory as above with the added constraints that the accelerations should be zero at the blend times.
Figure 7.24 (a) Trajectory with multiple quintic segments. (b) Velocity profile for multiple quintic segments. (c) Acceleration profile for multiple quintic segments.
7.6 Chapter Summary
In this chapter we studied methods for generating collision-free trajectories for robot manipulators. We divided the problem into two parts, first computing a collision-free path then by using interpolating polynomials to convert these paths into continuous trajectories.
We began by giving a more in-depth introduction to the concept of configuration space, including a catalog of configuration spaces for common robots and an explanation of how obstacles in the workspace map to configuration space obstacle regions. We described an algorithm to compute the configuration space obstacle region for the special case of a polygonal robot that translates in the plane (i.e., 
) in an environment populated by polygonal obstacles. For this special case, we introduced three planning algorithms that exploit three unique graph-based representations of the free configuration space: the visibility graph, the generalized Voronoi diagram, and the trapezoidal decomposition. These approaches are often applicable for problems that involve ground-based mobile robots.
For more complex robots, for example, robots that have high dimensional configuration spaces, we introduced algorithms that incrementally search the configuration space for a free path. The first such algorithm operates by constructing an artificial potential field whose negative gradient acts as a kind of artificial force that pushes the robot away from obstacles, while guiding it toward the goal configuration. We first developed this method for the case of 
, and then extended it to the more general case of non-Euclidean configuration spaces by using the relationship τ = JTF. In both cases, gradient descent was used as the method to guide the incremental exploration of the configuration space, and thus, for both cases, there are potential problems arising from the existence of multiple local minima in the field. We briefly described how random walks could be used to escape these local minima, and used this notion of randomization to motivate the development of sampling-based planning algorithms.
Sampling-based planners construct a roadmap in the configuration space using a random sampling scheme. We described two approaches: the probabilistic roadmap (PRM), and the rapidly-exploring random tree (RRT). For the PRM, a set of random samples is generated, and each of these samples is connected to a set of its nearest neighbors using a simple local motion planner (often a simple straight-line planner in the configuration space). Once the roadmap has been constructed, planning amounts to connecting the initial and goal configurations to the roadmap (again, using the simple, local planner), then searching the roadmap for a connecting path. In the case of RRTs, a random tree is grown from the start configuration by iteratively generating a random sample in the configuration space, then taking a small step toward this sample from its nearest neighbor in the current tree. Both of these methods have proven effective for a large variety of path planning problems.
Finally, we showed that, given a sequence of set points, a trajectory can be constructed using a low-order polynomial defined in terms of initial and final conditions for joint variables and their derivatives. We described cubic and quintic trajectories, along with trajectories that are pieced together from segments of constant acceleration (including minimum time, or bang-bang trajectories).
Problems
- Describe the configuration space for a mobile robot that can translate and rotate in the plane.
- Describe the configuration space for the three-link manipulator shown in Figure 3.12.
- Describe the configuration space for the two-link manipulator shown in Figure 3.13.
- Describe the configuration space for the two-link manipulator shown in Figure 3.14.
- Describe the configuration space for the three-link manipulator shown in Figure 3.15.
- Describe the configuration space for a six-link anthropomorphic arm equipped with a spherical wrist.
- Show that the visibility graph includes all shortest semi-free paths from
to 
. Note, this is equivalent to showing that a necessary condition for a path to be a shortest semi-free path is that it be included in the visibility graph. - Suppose
lies in the Voronoi region for a particular feature, f. Show that a straight-line path from 
that follows the gradient 
will arrive to a Voronoi edge before reaching any other feature f′. - Verify Equation (7.1).
- Derive the equations needed to compute the shortest distance from a point p to the line segment in the plane with vertices a1 and a2.
- Derive the equations needed to compute the shortest distance from a point p to the polygon in the plane with vertices ai, i = 1, …, n.
- Derive the equations needed to compute the shortest distance from a point p to the polygon in three dimensions with vertices ai, i = 1, …, n.
- Verify Equation (7.5).
- Consider a simple polygonal robot with four vertices, such that at q = (0, 0, 0) the vertices are located at a1(0) = (0, 0), a2(0) = (1, 0), a3(0) = (1, 1), and a4(0) = (0, 1). If two point obstacles are located at o1 = (3, 3) and o2 = ( − 3, −3), determine the artificial workspace and configuration space forces that act on the robot.
- Write a computer program to implement the path planner described in Section 7.3.2 for a three-link planar arm moving among polygonal obstacles.
- Write a simple computer program to perform collision checking for the case of a polygonal robot moving in the plane among polygonal obstacles. Your program should accept a configuration q as input, and should return a value that indicates whether q is a collision-free configuration.
- Give a procedure for generating random samples of orientations in SO(n) given that you have access to a random number generator that can generate samples from the uniform distribution on the unit interval. Your samples need not be uniformly distributed on SO(n).
- Write a computer program to implement the PRM planner described in Section 7.4.1 for a three-link planar arm moving among polygonal obstacles.
- Show by direct calculation that the determinant of the coefficient matrix in Equation (7.17) is (tf − t0)4.
- Suppose we wish a manipulator to start from an initial configuration at time t0 and track a conveyor. Discuss the steps needed in planning a suitable trajectory for this problem.
- Suppose we desire a joint space trajectory
for the ith joint (assumed to be revolute) that begins at rest at position q0 at time t0 and reaches position q1 in 2 seconds with a final velocity of 1 radian/sec. Compute a cubic polynomial satisfying these constraints. Sketch the trajectory as a function of time. - Compute a LSPB trajectory to satisfy the same requirements as in Problem 7–21. Sketch the resulting position, velocity, and acceleration profiles.
- Fill in the details of the computation of the LSPB trajectory. In other words, compute the portion of the trajectory between times tf − tb and tf and verify Equations (7.21).
- Write a Matlab m-file, lspb.m, to generate an LSPB trajectory, given appropriate initial data.
- Rewrite the Matlab m-files, cubic.m, quintic.m, and lspb.m to turn them into Matlab functions. Document them appropriately.
Notes and References
The earliest work on robot planning was done in the late sixties and early seventies in a few university-based Artificial Intelligence (AI) labs [40], [45], and [129]. This research dealt with high level planning using symbolic reasoning that was much in vogue at the time in the AI community. Geometry was not often explicitly considered in early robot planners, in part because it was not clear how to represent geometric constraints in a computationally feasible manner. The configuration space and its application to path planning were introduced in [97]. This was the first rigorous, formal treatment of the geometric path planning problem, and it initiated a surge in path planning research.
The earliest work in geometric path planning developed methods to construct volumetric representations of the free configuration space. These included exact methods [147], and approximate methods [20], [73], and [97]. In the former case, the best known algorithms have exponential complexity and require exact descriptions of both the robot and its environment, while in the latter case, the size of the representation of configuration space grows exponentially in the dimension of the configuration space. The best known algorithm for the path planning problem, giving an upper bound on the amount of computation time required to solve the problem, appeared in [21]. That real robots rarely have an exact description of the environment, and a drive for faster planning systems led to the development of potential fields approaches [77], and [79].
By the early nineties, a great deal of research had been done on the geometric path planning problem, and this work is nicely summarized in the textbook [87]. This textbook helped to generate a renewed interest in the path planning problem, and it provided a common framework in which to analyze and express path planning algorithms.
In the early nineties, randomization was introduced in the robot planning community [10], originally to circumvent the problems with local minima in potential fields. Early randomized motion planners proved effective for a large range of problems, but sometimes required extensive computation time for some robots in certain environments [75]. This limitation, together with the idea that a robot will operate in the same environment for a long period of time led to the development of the probabilistic roadmap planners [74, 132, 75]. Rapidly-exploring random trees were introduced in [90, 91].
Comprehensive reviews of motion planning research, including sensor-based approaches, can be found in [24, 88, 89].
Much work has been done in the area of collision detection in recent years [96], [115], [177], and [178]. This work is primarily focused on finding efficient, incremental methods for detecting collisions between objects when one or both are moving. A number of public domain collision detection software packages are currently available on the Internet.
Notes
- 1 An algorithm is said to be complete if it finds a solution whenever one exists, and signals failure in finite time when a solution does not exist.
- 2 Note that triangles are considered as trapezoids that have one side of length zero, and rectangles are special cases of trapezoids for which opposite sides are parallel.
- 3 Note that qi is used to denote the value of q at the ith iteration (not the ith component of the vector q).
- 4 A Gaussian density function is the classical bell shaped curve. The mean indicates the center of the curve (the peak of the bell) and the variance indicates the width of the bell. The probability density function (pdf) tells how likely it is that the variable qi will lie in a certain interval. The higher the pdf values, the more likely that qi will lie in the corresponding interval.
- 5 While there are some sampling-based planners that use quasi-random, or even deterministic sampling strategies, the use of randomized approaches is far more prevalent, and here we consider only these approaches.
- 6 A connected component is a maximal subgraph of the graph such that a path exists in the subgraph between any two vertices.
- 7 In the language of probability theory, the sample configurations correspond to independent random variables.
- 8 In Section 7.1.3 we used
to denote the initial configuration. In this section, we use q0 to denote the first configuration in a sequence of two or more configurations that will be used to define a path.