CHAPTER 5
INVERSE KINEMATICS

In Chapter 3 we showed how to determine the end effector’s position and orientation in terms of the joint variables. This chapter is concerned with the inverse problem, that of finding the joint variables in terms of the end effector’s position and orientation. This is the problem of inverse kinematics, and it is, in general, more difficult than the forward kinematics problem.

We begin by formulating the general inverse kinematics problem. Following this, we describe the principle of kinematic decoupling and how it can be used to simplify the inverse kinematics of most modern manipulators that are equipped with spherical wrists. Using kinematic decoupling, we can consider the position and orientation problems independently. We describe a geometric approach for solving the positioning problem, while we exploit the Euler angle parameterization to solve the orientation problem.

We also discuss numerical solution of the inverse kinematics using methods based on both the Jacobian inverse and the Jacobian transpose. The Jacobian inverse method is similar to a Newton–Raphson search whereas the Jacobian transpose method is a gradient search method.

5.1 The General Inverse Kinematics Problem

The general problem of inverse kinematics can be stated as follows. Given a 4 × 4 homogeneous transformation

(5.1)

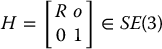
find a solution, or possibly multiple solutions, of the equation

(5.2)

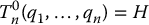
where

(5.3)

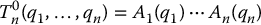
specifies the forward kinematics of an n-degree-of-freedom manipulator. Here the homogeneous transformation H represents the desired position and orientation of the end effector, and our task is to find the values for the joint variables q₁, …, q_n so that .

Equation (5.2) yields sixteen equations to be solved for the n unknown variables, q₁, …, q_n. However, since the bottom row of both and H are (0,0,0,1), four of these sixteen equations are trivial and so we can express the remaining twelve nonlinear equations as

(5.4)

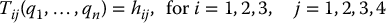
Example 5.1. (The Stanford Manipulator).

Recall the Stanford Manipulator of Section 3.3.5. Suppose that the desired position and orientation of the final frame are given by

(5.5)

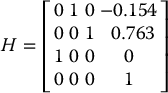
To find the corresponding joint variables θ₁, θ₂, d₃, θ₄, θ₅, and θ₆ we must solve the following simultaneous set of nonlinear trigonometric equations:

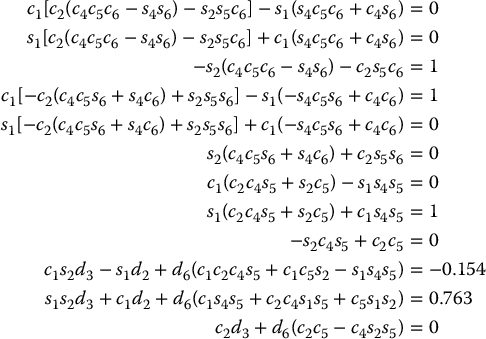
If the values of the nonzero DH parameters are d₂ = 0.154 and d₆ = 0.263, one solution to this set of equations is given by:

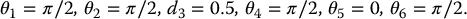
Even though we have not yet seen how one might derive this solution, it is not difficult to verify that it satisfies the forward kinematics equations for the Stanford Arm.

The equations in the preceding example are, of course, much too difficult to solve directly in closed form. This is the case for most robot arms. Therefore, we need to develop efficient and systematic techniques that exploit the particular kinematic structure of the manipulator. Whereas the forward kinematics problem always has a unique solution that can be obtained simply by evaluating the forward equations, the inverse kinematics problem may or may not have a solution. Even if a solution exists, it may or may not be unique. Furthermore, because these forward kinematic equations are in general complicated nonlinear functions of the joint variables, the solutions may be difficult to obtain even when they exist.

The inverse kinematics problem may be solved numerically or in closed form. Finding a closed-form solution means finding an explicit relationship

(5.6)

We first discuss the computation of closed-form solutions. In Section 5.5 we discuss numerical algorithms to find inverse kinematics solutions.

The practical question of the existence of solutions to the inverse kinematics problem depends on engineering as well as mathematical considerations. For example, the motion of the revolute joints may be restricted to less than a full 360 degrees of rotation so that not all mathematical solutions of the kinematic equations will correspond to physically realizable configurations of the manipulator. We will assume that the given position and orientation is such that at least one solution of Equation (5.2) exists. Once a solution to the mathematical equations is identified, it must be further checked to see whether or not it satisfies all constraints on the ranges of possible joint motions.

5.2 Kinematic Decoupling

Although the general problem of inverse kinematics is quite difficult, it turns out that for manipulators having six joints with three consecutive three joint axes intersecting at a point (such as the Stanford Manipulator above), it is possible to decouple the inverse kinematics problem into two simpler problems, known respectively as inverse position kinematics, and inverse orientation kinematics. To put it another way, for a six-DOF manipulator with a spherical wrist, the inverse kinematics problem may be separated into two simpler problems, namely, first finding the position of the intersection of the wrist axes, hereafter called the wrist center, and then finding the orientation of the wrist.

For concreteness let us suppose that there are exactly six degrees of freedom and that the last three joint axes intersect at a point . We express Equation (5.2) as two sets of equations representing the rotational and positional equations

(5.7)

(5.8)

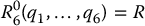
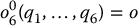
where and are the desired position and orientation of the tool frame, expressed with respect to the world coordinate system. Thus, we are given and , and the inverse kinematics problem is to solve for q₁, …, q₆.

The assumption of a spherical wrist means that the axes z₃, z₄, and z₅ intersect at and hence the origins and assigned by the DH convention will always be at the wrist center . Often will also be at , but this is not necessary for our subsequent development. The important point of this assumption for the inverse kinematics is that motion of the final three joints about these axes will not change the position of , and thus the position of the wrist center is a function of only the first three joint variables.

The origin of the tool frame (whose desired coordinates are given by ) is simply obtained by a translation of distance d₆ along z₅ from (see Table 3.3). In our case, z₅ and z₆ are the same axis, and the third column of expresses the direction of z₆ with respect to the base frame. Therefore, we have

(5.9)

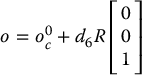
Thus, in order to have the end effector of the robot at the point with coordinates given by and with the orientation of the end effector given by , it is necessary and sufficient that the wrist center have coordinates given by

(5.10)

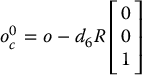
and that the orientation of the frame o₆x₆y₆z₆ with respect to the base be given by . If the components of the end effector’s position are denoted o_x, o_y, o_z and the components of the wrist center are denoted x_c, y_c, z_c then Equation (5.10) gives the relationship

(5.11)

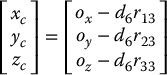
Using Equation (5.11) we may find the values of the first three joint variables. This determines the orientation transformation which depends only on these first three joint variables. We can now determine the orientation of the end effector relative to the frame o₃x₃y₃z₃ from the expression

(5.12)

(5.13)

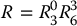
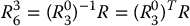
As we shall see in Section 5.4, the final three joint angles can then be found as a set of Euler angles corresponding to . Note that the right-hand side of Equation (5.13) is completely known since is given and can be calculated once the first three joint variables are known. The idea of kinematic decoupling is illustrated in Figure 5.1.

**Figure 5.1** Kinematic decoupling in the case of a spherical wrist. The vector *o_c* is the position of the wrist center point and o₆ is the position of the end effector, both with respect to the base frame. The wrist center point coordinates do not depend on the wrist orientation variables θ₄, θ₅, and θ₆.

5.3 Inverse Position: A Geometric Approach

For the most common kinematic arrangements that we consider, we can use a geometric approach to find the variables q₁, q₂, q₃ corresponding to given by Equation (5.10). Since most six-DOF manipulator designs are kinematically simple, usually consisting of one of the five basic configurations of Chapter 1 with a spherical wrist, the geometric approach is simple and effective. Indeed, it is partly due to the difficulty of the general inverse kinematics problem that manipulator designs have evolved to their present state.

In general, the complexity of the inverse kinematics problem increases with the number of nonzero DH parameters. For most manipulators, many of the a_i, d_i are zero, the α_i are 0 or ± π/2, etc. In these cases especially, a geometric approach is the simplest and most natural. The general idea of the geometric approach is to solve for joint variable q_i by projecting the manipulator onto the x_{i − 1} − y_{i − 1} plane and solving a simple trigonometry problem. For example, to solve for θ₁, we project the arm onto the x₀ − y₀ plane and use trigonometry to find θ₁. We will illustrate this method with two important examples: the spherical (RRP) and the articulated (RRR) arms.

5.3.1 Spherical Configuration

We first solve the inverse position kinematics for a three degree of freedom spherical manipulator shown in Figure 5.2, with the components of denoted by x_c, y_c, z_c. Projecting onto the x₀ − y₀ plane, we see that

A free body diagram shows the inverse position kinematics for a three degree of freedom spherical manipulator. — **Figure 5.2** First three joints of a spherical manipulator.

(5.14)

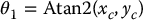
in which Atan2 denotes the two-argument arctangent function defined in Appendix A. Note that a second valid solution for θ₁ is

(5.15)

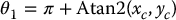
Of course, this will, in turn, lead to a different solution for θ₂.

These solutions for θ₁, are valid unless x_c = y_c = 0. In this case, Equation (5.14) is undefined and the manipulator is in a singular configuration, in which the wrist center intersects z₀ as shown in Figure 5.3. In this configuration any value of θ₁ leaves fixed. There are thus infinitely many solutions for θ₁ when intersects z₀.

A free body diagram shows the singular configuration for a spherical manipulator in which the wrist center lies on the z subscript 0 axis. — **Figure 5.3** Singular configuration for a spherical manipulator in which the wrist center lies on the z₀ axis.

The angle θ₂ is given from Figure 5.2 as

(5.16)

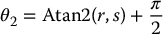
where r² = x²_c + y_c² and x = z_c − d₁.

The linear distance d₃ is found as

(5.17)

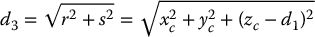
The negative square root solution for d₃ is disregarded and thus in this case we obtain two solutions to the inverse position kinematics as long as the wrist center does not intersect z₀.

5.3.2 Articulated Configuration

We next consider the elbow manipulator shown in Figure 5.4, As in the case of the spherical manipulator, the first joint variable is the base rotation and there are two possible solutions

A free body diagram shows the elbow manipulator (spherical) with first three joints. — **Figure 5.4** First three joints of an elbow manipulator.

(5.18)

(5.19)

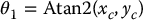
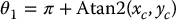
provided x_c and y_c are not both zero.

If both x_c and y_c are zero, as shown in Figure 5.5, the configuration is singular as before and θ₁ may take on any value.

A free body diagram shows the singular configuration for an elbow manipulator in which the wrist center lies on the z subscript 0 axis. — **Figure 5.5** Singular configuration for an elbow manipulator in which the wrist center lies on the z₀ axis.

If there is an offset d ≠ 0 as shown in Figure 5.6 then the wrist center cannot intersect z₀. In this case, depending on how the DH parameters have been assigned, we will have d₂ = d or d₃ = d, and there will, in general, be only two solutions for θ₁.

A free body diagram shows the elbow manipulator with shoulder offset. — **Figure 5.6** Elbow manipulator with shoulder offset.

These correspond to the so-called left arm and right arm configurations as shown in Figures 5.7.

Two free body diagrams show the left arm (on the left-hand side) and right arm (on the right-hand side) configurations for an elbow manipulator with an offset. — **Figure 5.7** Left arm (left) and right arm (right) configurations for an elbow manipulator with an offset.

For the left arm configuration in Figure 5.7 we see geometrically that

(5.20)

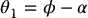
in which

(5.21)

(5.22)

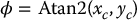
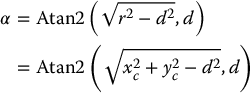
The second solution, given by the right arm configuration in Figure 5.7 is given by

(5.23)

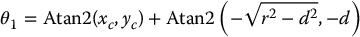
To see this, note that

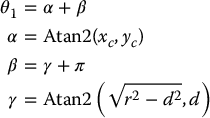
which together imply that

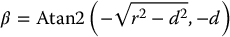
since cos (θ + π) = −cos (θ) and sin (θ + π) = −sin (θ).

To find the angles θ₂, θ₃ for the elbow manipulator given θ₁, we consider the plane formed by the second and third links as shown in Figure 5.8. Since the motion of second and third links is planar, the solution is analogous to that of the two-link manipulator of Chapter 1. As in our previous derivation (cf. Equations (1.10) and (1.11)), we can apply the law of cosines to obtain

(5.24)

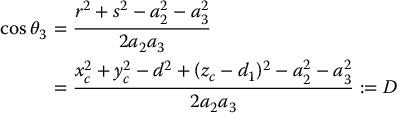
since r² = x²_c + y_c² − d² and s = z_c − d₁. Hence, θ₃ is given by

(5.25)

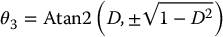
The two solutions for θ₃ correspond to the elbow down position and elbow up position, respectively. Similarly θ₂ is given as

(5.26)

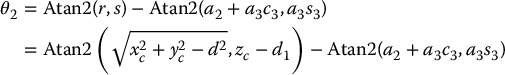
A free body diagram shows the formation of plane by the second and third links. — **Figure 5.8** Projecting onto the plane formed by links 2 and 3.

An example of an elbow manipulator with offsets is the PUMA shown in Figure 5.9. There are four solutions to the inverse position kinematics as shown. These correspond to the situations left arm–elbow up, left arm–elbow down, right arm–elbow up and right arm–elbow down. We will see that there are two solutions for the wrist orientation thus giving a total of eight solutions of the inverse kinematics for the PUMA manipulator.

The diagram shows four solutions (left arm elbow up, right arm elbow up, left arm elbow down and right arm elbow down) of the inverse position kinematics for the PUMA manipulator. — **Figure 5.9** Four solutions of the inverse position kinematics for the PUMA manipulator.

5.4 Inverse Orientation

In the previous section we used a geometric approach to solve the inverse position problem. This gives the values of the first three joint variables corresponding to a given position of the wrist center. The inverse orientation problem is now one of finding the values of the final three joint variables corresponding to a given orientation with respect to the frame o₃x₃y₃z₃. For a spherical wrist, this can be interpreted as the problem of finding a set of Euler angles corresponding to a given rotation matrix . Recall that Equation (3.15) shows that the rotation matrix obtained for the spherical wrist has the same form as the rotation matrix for the Euler transformation given in Equation (2.27). Therefore, we can use the method developed in Section 2.5.1 to solve for the three joint angles of the spherical wrist. In particular, we solve for the three Euler angles, ϕ, θ, ψ, using Equations (2.29)–(2.34), and then use the mapping

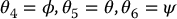
Example 5.2. (Articulated Manipulator with Spherical Wrist).

The DH parameters for the frame assignment shown in Figure 5.4 are summarized in Table 5.1. Multiplying the corresponding A_i matrices gives the matrix for the articulated or elbow manipulator as

(5.27)

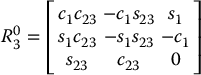
The matrix is the upper left 3 × 3 submatrix of the matrix product A₄A₅A₆ given by

(5.28)

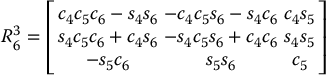
The equation to be solved for the final three variables is therefore

(5.29)

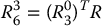
and the Euler angle solution can be applied to this equation. For example, the three equations given by the third column in the above matrix equation are given by

(5.30)

(5.31)

(5.32)

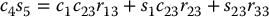
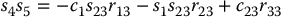
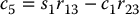
Hence, if both of Equations (5.30) and (5.31) are not zero, we obtain θ₅ from Equations (2.29) and (2.30) as

(5.33)

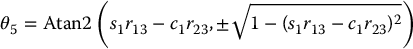
If the positive square root is chosen in Equation (5.33), then θ₄ and θ₆ are given by Equations (2.31) and (2.32), respectively, as

(5.34)

(5.35)

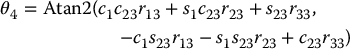
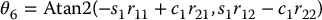
The other solutions are obtained analogously. If s₅ = 0, then joint axes z₃ and z₅ are collinear. This is a singular configuration and only the sum θ₄ + θ₆ can be determined. One solution is to choose θ₄ arbitrarily and then determine θ₆ using Equation (2.36) or (2.38).

Example 5.3. (Elbow Manipulator — Complete Solution).

To summarize the geometric approach for solving the inverse kinematics equations, we give here one solution to the inverse kinematics of the six degree-of-freedom elbow manipulator shown in Figure 5.4, which has no joint offsets and a spherical wrist.

Given

(5.36)

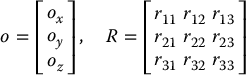
then with

(5.37)

(5.38)

(5.39)

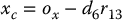
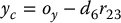
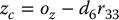
a set of DH joint variables is given by

(5.40)

(5.41)

(5.42)

(5.43)

(5.44)

(5.45)

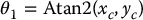
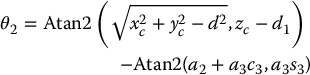
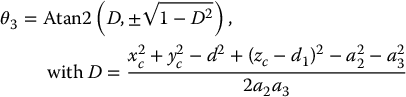
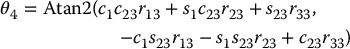
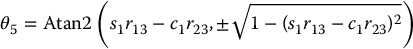
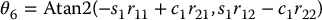
The other possible solutions are left as an exercise (Problem 5–10).

Example 5.4. (SCARA Manipulator).

As another example, consider the SCARA manipulator illustrated in Figure 5.10, with forward kinematics defined by from Equation (3.24). The inverse kinematics solution is then given as the set of solutions of the equation

(5.46)

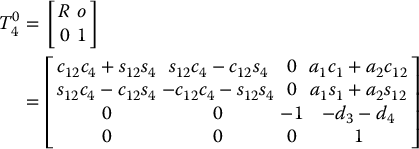
We first note that, since the SCARA has only four degrees of freedom, not every possible H from SE(3) allows a solution of Equation (5.46). In fact we can easily see that there is no solution of Equation (5.46) unless is of the form

(5.47)

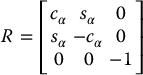
and if this is the case, the sum θ₁ + θ₂ − θ₄ is determined by

(5.48)

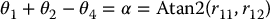
Projecting the manipulator configuration onto the x₀ − y₀ plane yields the geometry shown in Figure 5.10. Using the law of cosines

(5.49)

(5.50)

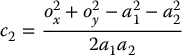
and

(5.51)

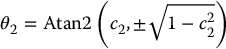
The value for θ₁ is then obtained as

(5.52)

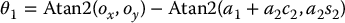
We may now determine θ₄ from Equation (5.48) as

(5.53)

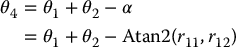
Finally d₃ is given as

(5.54)

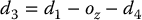
A free body diagram shows the first three joints of a SCARA manipulator. — **Figure 5.10** First three joints of a SCARA manipulator.

Table 5.1 DH parameters for the articulated manipulator of Figure 5.4.

Link	a_i	α_i	d_i	θ_i
1	0	90	d₁	θ₁
2	a₂	0	0	θ₂
3	a₃	0	0	θ₃

5.5 Numerical Inverse Kinematics

For the manipulators considered in the previous sections we derived closed-form solutions for the inverse kinematics. In this section, we consider iterative, numerical algorithms for the computation of the inverse kinematics. Numerical methods are increasingly popular due to the availability of high-performance computation and the advent of open-source software. In addition, in cases where closed-form solutions do not exist, or if the manipulator is redundant, a recourse to numerical methods may be the better option.

Let be a vector of Cartesian coordinates. For example, x^d could represent the wrist center point (m = 3) or the end-effector position and orientation using a minimal representation for the end-effector orientation (m = 6). The forward kinematics for an n-link manipulator, in this case, is a function . If we set

(5.55)

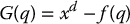
then a solution to the inverse kinematics is a configuration q^d satisfying G(q^d) = x^d − f(q^d) = 0. Below we will give details of the most common algorithms to iteratively solve for q^d given x^d; the first based on the Jacobian inverse, which is similar to the Newton–Raphson method for root finding, and the second is based on the Jacobian transpose and is derived as a gradient search algorithm.

Jacobian Inverse Method

With x^d given as a desired robot configuration, we expand the forward kinematics function f(q) in a Taylor series about a configuration q^d, where x^d = f(q^d) to obtain

(5.56)

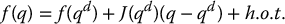
where we take J = J_a(q) as the analytic Jacobian in Equation (4.83). Neglecting the higher order terms (h.o.t.), we have

(5.57)

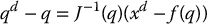
assuming that the Jacobian is square and invertible. To find a solution for q^d, we begin with an initial guess, q₀, and form a sequence of successive estimates, q₀, q₁, q₂, …, as

(5.58)

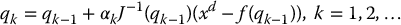
Note that we have introduced a step size, α_k > 0, into the equation, which can be adjusted to aid convergence. The step size α_k may be chosen as a constant or as a function of k, a scalar or as a diagonal matrix, the last in order to scale each component of the configuration separately.

Remark 5.1.

Since Equation (5.57) is based on a first-order approximation of the inverse kinematics, only local convergence can be expected. Also, since there are generally multiple solutions to the inverse kinematics, the particular configuration that results from running the algorithm is dependent on the initial guess.

Figure (5.11) shows the results obtained for a two-link, planar RR manipulator. The algorithm converges to within 10^{− 4} of the exact solution after 10 iterations with the given parameters.

The figure shows a graph on the left-hand side and a three-column table on the right-hand side. Both are illustarting the inverse kinematics solution using the Jacobian inverse. — **Figure 5.11** Inverse kinematics solution using the Jacobian inverse. Desired end-effector coordinates are *x^d* = (0.2, 1.3). The joint variables corresponding to *x^d* are θ₁ = 0.5650, θ₂ = 1.7062. The initial guess is θ₁ = 0.25, θ₂ = 0.75. The step size α was chosen as 0.75.

If the Jacobian is not square or not invertible, then one may use the pseudoinverse J† = J†_a in place of J^{− 1}_a. For m ⩽ n, we defined the right pseudoinverse in Appendix B as J† = J^T(JJ^T)^{− 1}. In this case, we can define the update rule for q_k as

(5.59)

Jacobian Transpose Method

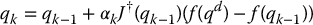
The second method that we outline is based on the Jacobian transpose J^T(q) instead of the Jacobian inverse. To begin, we define an optimization problem

(5.60)

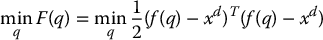
where, as above, x^d is the desired configuration and f(q) is the forward kinematics map. The gradient of the above cost function F(q) is given by

(5.61)

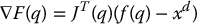
A gradient descent algorithm to minimize F(q) (see Appendix D) is then

(5.62)

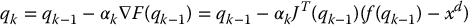
where, again, α_k > 0 is the step size.

Remark 5.2.

An advantage of this method is that the Jacobian transpose is easier to compute than the Jacobian inverse and does not suffer from configuration singularities. In general, however, the convergence, in terms of number of iterations, may be slower with this method.

Figure 5.12 shows the response for the two-link RR manipulator for the same desired configuration and initial guess as in Figure 5.11. In this case, the algorithm converges after 30 iterations.

The figure shows a graph on the left-hand side and a three-column table on the right-hand side. It illustrates the response for the two-link RR manipulator for the same desired configuration and initial guess. — **Figure 5.12** Inverse kinematics solution using the Jacobian transpose. Desired end-effector coordinates are *x^d* = (0.2, 1.3). The joint variables corresponding to *x^d* are θ₁ = 0.5650, θ₂ = 1.7062. The initial guess is θ₁ = 0.25, θ₂ = 0.75. The step size α was chosen as 0.75.

5.6 Chapter Summary

This DH convention defines the forward kinematics equations for a manipulator, i.e., the mapping from joint variables to end effector position and orientation. To control a manipulator, it is necessary to solve the inverse problem, i.e., given a position and orientation for the end effector, solve for the corresponding set of joint variables.

In this chapter we considered the special case of manipulators for which kinematic decoupling can be used (e.g., a manipulator with a spherical wrist). For this class of manipulators the determination of the inverse kinematics can be summarized by the following algorithm.

Step 1: Find q₁, q₂, q₃ such that the wrist center has coordinates given by

(5.63)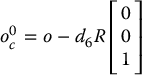
Step 2: Using the joint variables determined in Step 1, evaluate .
Step 3: Find a set of Euler angles corresponding to the rotation matrix

(5.64)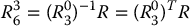

We demonstrated a geometric approach for Step 1. In particular, to solve for joint variable q_i, we project the manipulator (including the wrist center) onto the x_{i − 1} − y_{i − 1} plane and use trigonometry to find q_i.

We also discuss numerical methods for computing the inverse kinematics using the inverse Jacobian and the Jacobian transpose. The Jacobian inverse kinematics algorithm takes the form

(5.65)

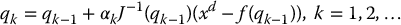
The Jacobian transpose inverse kinematics algorithm takes the form

(5.66)

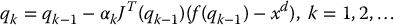
Problems

Given a desired position of the end effector, how many solutions are there to the inverse kinematics of the three-link planar arm shown in Figure 5.13? If the orientation of the end effector is also specified, how many solutions are there? Use any method in this chapter to characterize the inverse kinematics.
Repeat Problem 5–1 for the three-link planar arm with prismatic joint of Figure 5.14.
Solve the inverse position kinematics for the cylindrical manipulator of Figure 5.15.
Solve the inverse position kinematics for the Cartesian manipulator of Figure 5.16.
Add a spherical wrist to the three-link cylindrical arm of Problem 5–3 and write the complete inverse kinematics solution.
Add a spherical wrist to the Cartesian manipulator of Problem 5–4 and write the complete inverse kinematics solution.
Write a computer program to compute the inverse kinematic equations for the elbow manipulator using Equations (5.40)–(5.45). Include procedures for identifying singular configurations and choosing a particular solution when the configuration is not singular. Test your routine for various special cases, including singular configurations.
The Stanford manipulator of Example 3.3.5 has a spherical wrist. Given a desired position and orientation of the end effector,
1. Compute the desired coordinates of the wrist center .
2. Solve the inverse position kinematics, that is, find values of the first three joint variables that will place the wrist center at . Is the solution unique? How many solutions did you find?
3. Compute the rotation matrix . Solve the inverse orientation problem for this manipulator by finding a set of Euler angles corresponding to given by Equation (5.28).
Repeat Problem 5–8 for the PUMA 260 manipulator of Problem 5–9, which also has a spherical wrist. How many total solutions did you find?
Find all other solutions to the inverse kinematics of the elbow manipulator of Section 5.3.2.
Modify the solutions θ₁ and θ₂ for the spherical manipulator given by Equations (5.15) and (5.16) for the case of a shoulder offset.

The figure shows the three-link planar robot with revolute joints. — **Figure 5.13** Three-link planar robot with revolute joints.

The figure shows the three-link planar robot with prismatic joint. — **Figure 5.14** Three-link planar robot with prismatic joint.

A free body diagram shows an example of the cylindrical configuration. — **Figure 5.15** Cylindrical configuration.

A free body diagram shows an example of the Cartesian configuration. — **Figure 5.16** Cartesian configuration.

Notes and References

The problem of inverse kinematics is classical and predates robotics by several hundred years. Consequently there is an extensive literature dealing with inverse kinematics within and without the robotics communities. An early fundamental result in robotics was the work of Pieper [137], who showed that any 6 DOF robot with at least three consecutive joint axes intersecting at a common point has a closed-form solution to the inverse kinematics. This property of robot kinematics is, in fact, the main reason for the importance of the spherical wrist. The approach that we use here of partitioning the inverse kinematics into inverse position and inverse orientation in the case of a spherical wrist is due to Hollerbach and Gideon [65]. We showed that the PUMA robot has 8 distinct inverse kinematic solutions. Primrose [139] gave an explicit upper bound of 16 for the number of inverse kinematic solutions for a general 6 DOF manipulator. This is a hard bound as shown by Manseur and Doty [108], who gave an example of a robot with 16 solutions. Although we do not treat the kinematics of parallel robots in this text, it turns out that the inverse kinematics problem for parallel robots is easier than it is for serial-link robots [68]. Numerical solutions to the inverse kinematics problem is treated in several sources, for example, [176] and [54]. Other good references for inverse kinematics of manipulators are, for example, [7], [92], [93], [135], [148], [119], and [105].