CHAPTER 3
FORWARD KINEMATICS
The problem of manipulator kinematics is to describe the motion of a manipulator without consideration of the forces and torques causing the motion. The kinematic description is therefore a geometric one. In this chapter we consider the forward kinematics problem for serial link manipulators, which is to determine the position and orientation of the end effector given the values for the joint variables of the robot. This problem is easily solved by attaching coordinate frames to each link of the robot and expressing the relationships among these frames as homogeneous transformations. We use a systematic procedure, known as the Denavit–Hartenberg convention, to attach these coordinate frames to the robot. The position and orientation of the robot end effector is then reduced to a matrix multiplication of homogeneous transformations. We give examples of this procedure for several of the standard configurations that we introduced in Chapter 1.
In subsequent chapters we will consider the problems of velocity kinematics and inverse kinematics. The former problem is to determine the relation between the end-effector velocity and the joint velocities whereas the inverse kinematics problem is to determine the joint variables given the end-effector position and orientation.
3.1 Kinematic Chains
As described in Chapter 1, a robot manipulator is composed of a set of links connected together by joints. The joints can either be very simple, such as a revolute joint or a prismatic joint, or they can be more complex, such as a ball and socket joint (recall that a revolute joint is like a hinge that allows a relative rotation about a single axis, and a prismatic joint permits a linear motion along a single axis, namely an extension or retraction). The difference between the two situations is that in the first instance the joint has only a single degree-of-freedom of motion: the angle of rotation in the case of a revolute joint, and the amount of linear displacement in the case of a prismatic joint. In contrast, a ball and socket joint has two degrees of freedom. In this book it is assumed throughout that all joints have only a single degree of freedom. This assumption does not involve any real loss of generality, since joints such as a ball and socket joint (two degrees of freedom) or a spherical wrist (three degrees of freedom) can always be thought of as a succession of single degree-of-freedom joints with links of length zero in between.
With the assumption that each joint has a single degree-of-freedom, the action of each joint can be described by a single real number: the angle of rotation in the case of a revolute joint or the displacement in the case of a prismatic joint.
A robot manipulator with n joints will have n + 1 links, since each joint connects two links. We number the joints from 1 to n, and we number the links from 0 to n, starting from the base. By this convention, joint i connects link i − 1 to link i. We will consider the location of joint i to be fixed with respect to link i − 1. When joint i is actuated, link i moves. Therefore, link 0 (the first link or base) is fixed, and does not move when the joints are actuated. Of course, the robot manipulator could itself be mobile (e.g., it could be mounted on a mobile platform or on an autonomous vehicle), but we will not consider this case in the present chapter, since it can be handled easily by slightly extending the techniques presented here.
With the ith joint, we associate a joint variable, denoted by qi. In the case of a revolute joint, qi is the angle of rotation, and in the case of a prismatic joint, qi is the joint displacement:
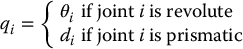
To perform the kinematic analysis, we attach a coordinate frame rigidly to each link. In particular, we attach oixiyizi to link i. This means that, whatever motion the robot executes, the coordinates of each point on link i are constant when expressed in the ith coordinate frame. Furthermore, when joint i is actuated, link i and its attached frame, oixiyizi, experience a resulting motion. The frame o0x0y0z0, which is attached to the robot base, is referred to as the base frame, inertial frame or world frame. Figure 3.1 illustrates the idea of attaching frames rigidly to links in the case of an elbow manipulator.

Figure 3.1 Coordinate frames attached to elbow manipulator.
Now, suppose Ai is the homogeneous transformation matrix that gives the position and orientation of oixiyizi with respect to oi − 1xi − 1yi − 1zi − 1. The matrix Ai is not constant, but varies as the configuration of the robot is changed. However, the assumption that all joints are either revolute or prismatic means that Ai is a function of only a single joint variable, namely qi. In other words,
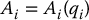
The homogeneous transformation matrix that expresses the position and orientation of ojxjyjzj with respect to oixiyizi is called a transformation matrix, and is denoted by  . From Chapter 2 we see that
. From Chapter 2 we see that
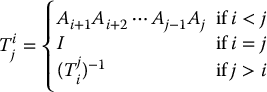
By the manner in which we have rigidly attached the various frames to the corresponding links, it follows that the position of any point on the end effector when expressed in the last frame n is a constant independent of the configuration of the robot. We denote the position and orientation of the end effector with respect to the inertial or base frame by a three-vector  (which gives the coordinates of the origin of the end-effector frame with respect to the base frame) and the 3 × 3 rotation matrix
(which gives the coordinates of the origin of the end-effector frame with respect to the base frame) and the 3 × 3 rotation matrix  , and define the homogeneous transformation matrix
, and define the homogeneous transformation matrix
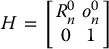
Then the position and orientation of the end effector in the inertial frame are given by the product
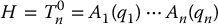
Each homogeneous transformation Ai is of the form
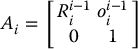
Hence, for i < j
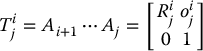
The matrix  expresses the orientation of ojxjyjzj relative to oixiyizi and is given by the rotational parts of the A matrices as
expresses the orientation of ojxjyjzj relative to oixiyizi and is given by the rotational parts of the A matrices as
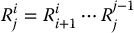
The coordinate vectors  are given recursively by the formula
are given recursively by the formula
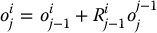
These expressions will be useful in Chapter 4 when we study Jacobian matrices.
In principle, that is all there is to forward kinematics; determine the functions Ai(qi), and multiply them together as needed. However, it is possible to achieve a considerable amount of streamlining and simplification by introducing further conventions, such as the Denavit–Hartenberg representation of a joint, and this is the objective of the next section.
3.2 The Denavit–Hartenberg Convention
In this section we develop a set of conventions that provide a systematic procedure for computing the forward kinematic equations. It is, of course, possible to carry out forward kinematics analysis even without respecting these conventions, as we did for the two-link planar manipulator example in Chapter 1. However, the kinematic analysis of an n-link manipulator can be extremely complex and the conventions introduced below simplify the analysis considerably. Moreover, they give rise to a universal language with which engineers can communicate.
A commonly used convention for selecting frames of reference in robotic applications is the Denavit–Hartenberg, or DH convention. In this convention, each homogeneous transformation Ai is represented as a product of four basic transformations
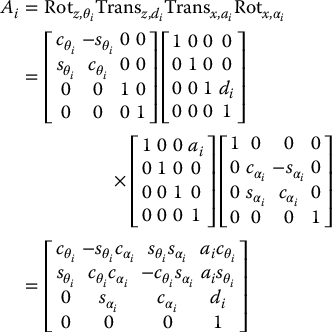
where the four quantities θi, ai, di, αi are parameters associated with link i and joint i. The four parameters ai, αi, di, and θi in Equation (3.10) are generally given the names link length, link twist, link offset, and joint angle, respectively. These names derive from specific aspects of the geometric relationship between two coordinate frames, as will become apparent below. Since the matrix Ai is a function of a single variable, three of the above four quantities are constant for a given link, while the fourth parameter, θi for a revolute joint and di for a prismatic joint, is the joint variable.
From Chapter 2 one can see that an arbitrary homogeneous transformation matrix can be characterized by six numbers, for example, three numbers to specify the fourth column of the matrix and three Euler angles to specify the upper left 3 × 3 rotation matrix. In the DH representation, in contrast, there are only four parameters. How is this possible? The answer is that, while frame i is required to be rigidly attached to link i, we have considerable freedom in choosing the origin and the coordinate axes of the frame. For example, it is not necessary that the origin  of frame i be placed at the physical end of link i. In fact, it is not even necessary that frame i be placed within the physical link. Frame i could lie in free space so long as frame i is rigidly attached to link i. By a clever choice of the origin and the coordinate axes, it is possible to cut down the number of parameters needed from six to four (or even fewer in some cases). In Section 3.2.1 we will show why, and under what conditions, this can be done, and in Section 3.2.2 we will show exactly how to make the coordinate frame assignments.
of frame i be placed at the physical end of link i. In fact, it is not even necessary that frame i be placed within the physical link. Frame i could lie in free space so long as frame i is rigidly attached to link i. By a clever choice of the origin and the coordinate axes, it is possible to cut down the number of parameters needed from six to four (or even fewer in some cases). In Section 3.2.1 we will show why, and under what conditions, this can be done, and in Section 3.2.2 we will show exactly how to make the coordinate frame assignments.
3.2.1 Existence and Uniqueness
Clearly it is not possible to represent any arbitrary homogeneous transformation using only four parameters. Therefore, we begin by determining just which homogeneous transformations can be expressed in the form given by Equation (3.10). Suppose we are given two frames, denoted by frames 0 and 1, respectively. Then there exists a unique homogeneous transformation matrix A that takes the coordinates from frame 1 into those of frame 0. Now, suppose the two frames have the following two additional features:
- (DH1) The axis x1 is perpendicular to the axis z0.
- (DH2) The axis x1 intersects the axis z0.
These two properties are illustrated in Figure 3.2. Under these conditions, we claim that there exist unique numbers a, d, θ, α such that

Figure 3.2 Coordinate frames satisfying assumptions DH1 and DH2.
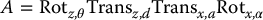
Of course, since θ and α are angles, we really mean that they are unique to within a multiple of 2π. To show that the matrix A can be written in this form, write A as

If (DH1) is satisfied, then x1 is perpendicular to z0 and we have x1 · z0 = 0. Expressing this constraint with respect to o0x0y0z0, using the fact that the first column of  is the representation of the unit vector x1 with respect to frame 0, we obtain
is the representation of the unit vector x1 with respect to frame 0, we obtain
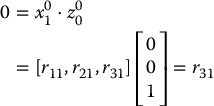
Since r31 = 0, we now need only show that there exist unique angles θ and α such that
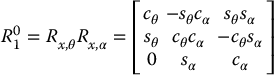
The only information we have is that r31 = 0, but this is enough. First, since each row and column of  must have unit length, r31 = 0 implies that
must have unit length, r31 = 0 implies that

Hence, there exist unique θ and α such that
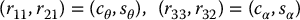
So far, we have shown that
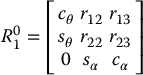
Again, using the fact that  is a rotation matrix, we must have
is a rotation matrix, we must have
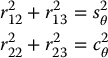
Since these equations must hold for all values of θ, in particular for θ = 0, π, we must also have
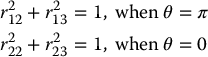
Putting these expressions together, we can write these variables as
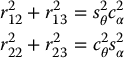
which are satisfied by taking r12, r13, r22, and r23 as in Equation (3.13).
Next, assumption (DH2) means that the displacement between  and
and  can be expressed as a linear combination of the vectors z0 and x1. This can be written as
can be expressed as a linear combination of the vectors z0 and x1. This can be written as  . Again, we can express this relationship in the coordinates of o0x0y0z0, and we obtain
. Again, we can express this relationship in the coordinates of o0x0y0z0, and we obtain
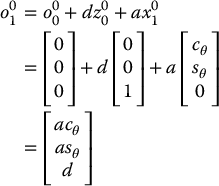
Combining the above results, we obtain Equation (3.10) as claimed. Thus, we see that four parameters are sufficient to specify any homogeneous transformation that satisfies the constraints (DH1) and (DH2).
Now that we have established that each homogeneous transformation matrix satisfying conditions (DH1) and (DH2) above can be expressed as in Equation (3.10), we can give a physical interpretation to each of these four quantities. The parameter a is the distance between the axes z0 and z1, and is measured along the axis x1. The angle α is the angle between the axes z0 and z1, measured in a plane normal to x1. The positive sense for α is determined from z0 to z1 by the right hand rule as shown in Figure 3.3. The parameter d is the distance from the origin  to the intersection of the x1 axis with z0 measured along the z0 axis. Finally, θ is the angle from x0 to x1 measured in a plane normal to z0. These physical interpretations will prove useful in developing a procedure for assigning coordinate frames that satisfy the constraints (DH1) and (DH2), and we now turn our attention to developing such a procedure.
to the intersection of the x1 axis with z0 measured along the z0 axis. Finally, θ is the angle from x0 to x1 measured in a plane normal to z0. These physical interpretations will prove useful in developing a procedure for assigning coordinate frames that satisfy the constraints (DH1) and (DH2), and we now turn our attention to developing such a procedure.

Figure 3.3 Positive sense for αi and θi.
3.2.2 Assigning the Coordinate Frames
For a given robot manipulator, one can always choose the frames 0, …, n in such a way that the above two conditions are satisfied. In certain circumstances, this will require placing the origin  of frame i in a location that may not be intuitively satisfying, but typically this will not be the case. In reading the material below, it is important to keep in mind that the choices of the various coordinate frames are not unique, even when constrained by the requirements above. Thus, it is possible that different engineers will derive differing, but equally correct, coordinate frame assignments for the links of the robot. It is very important to note, however, that the end result (i.e., the matrix
of frame i in a location that may not be intuitively satisfying, but typically this will not be the case. In reading the material below, it is important to keep in mind that the choices of the various coordinate frames are not unique, even when constrained by the requirements above. Thus, it is possible that different engineers will derive differing, but equally correct, coordinate frame assignments for the links of the robot. It is very important to note, however, that the end result (i.e., the matrix  ) will be the same, regardless of the assignment of intermediate DH frames (assuming that the coordinate frames for links 0 and n coincide). We begin by deriving the general procedure. We then discuss various common special cases for which it is possible to further simplify the homogeneous transformation matrix.
) will be the same, regardless of the assignment of intermediate DH frames (assuming that the coordinate frames for links 0 and n coincide). We begin by deriving the general procedure. We then discuss various common special cases for which it is possible to further simplify the homogeneous transformation matrix.
To start, note that the choice of zi is arbitrary. In particular, from Equation (3.13), we see that by choosing αi and θi appropriately, we can obtain any arbitrary direction for zi. Thus, for our first step, we assign the axes z0, …, zn − 1 in an intuitively pleasing fashion. Specifically, we assign zi to be the axis of actuation for joint i + 1. Thus, z0 is the axis of actuation for joint 1, z1 is the axis of actuation for joint 2, etc. There are two cases to consider: (i) if joint i + 1 is revolute, zi is the axis of revolution of joint i + 1; (ii) if joint i + 1 is prismatic, zi is the axis of translation of joint i + 1. At first it may seem a bit confusing to associate zi with joint i + 1, but recall that this satisfies the convention that we established above, namely that when joint i is actuated, link i and its attached frame, oixiyizi, experience a resulting motion.
Once we have established the z-axes for the links, we establish the base frame. The choice of a base frame is nearly arbitrary. We may choose the origin  of the base frame to be any point on z0. We then choose x0, y0 in any convenient manner so long as the resulting frame is right-handed. This sets up frame 0.
of the base frame to be any point on z0. We then choose x0, y0 in any convenient manner so long as the resulting frame is right-handed. This sets up frame 0.
Once frame 0 has been established, we begin an iterative process in which we define frame i using frame i − 1, beginning with frame 1. Figure 3.4 will be useful for understanding the process that we now describe.

Figure 3.4 Denavit–Hartenberg frame assignment.
In order to set up frame i it is convenient to consider three cases: (i) the axes zi − 1, zi are not coplanar, (ii) the axes zi − 1, zi intersect, (iii) the axes zi − 1, zi are parallel. Note that in both cases (ii) and (iii) the axes zi − 1 and zi are coplanar. This situation is in fact quite common, as we will see in Section 3.3. We now consider each of these three cases.
(i) zi − 1 and zi are not coplanar: If zi − 1 and zi are not coplanar, then there exists a unique shortest line segment from zi − 1 to zi, perpendicular to both zi − 1 to zi. This line segment defines xi, and the point where it intersects zi is the origin  . By construction, both conditions (DH1) and (DH2) are satisfied and the vector from
. By construction, both conditions (DH1) and (DH2) are satisfied and the vector from  to
to  is a linear combination of zi − 1 and xi. The specification of frame i is completed by choosing the axis yi to form a right-handed frame. Since assumptions (DH1) and (DH2) are satisfied, the homogeneous transformation matrix Ai is of the form given in Equation (3.10).
is a linear combination of zi − 1 and xi. The specification of frame i is completed by choosing the axis yi to form a right-handed frame. Since assumptions (DH1) and (DH2) are satisfied, the homogeneous transformation matrix Ai is of the form given in Equation (3.10).
(ii) zi − 1 is parallel to zi: If the axes zi − 1 and zi are parallel, then there are infinitely many common normals between them and condition (DH1) does not specify xi completely. In this case we are free to choose the origin  at any convenient point on the zi-axis. The axis xi is then chosen either to be directed from
at any convenient point on the zi-axis. The axis xi is then chosen either to be directed from  toward zi − 1, along the common normal, or as the opposite of this vector. A common method for choosing
toward zi − 1, along the common normal, or as the opposite of this vector. A common method for choosing  is to choose the normal that passes through
is to choose the normal that passes through  as the xi axis;
as the xi axis;  is then the point at which this normal intersects zi. In this case, di would be equal to zero. Once xi is fixed, yi is determined, as usual by the right hand rule. Since the axes zi − 1 and zi are parallel, αi will be zero in this case.
is then the point at which this normal intersects zi. In this case, di would be equal to zero. Once xi is fixed, yi is determined, as usual by the right hand rule. Since the axes zi − 1 and zi are parallel, αi will be zero in this case.
(iii) zi − 1 intersects zi: In this case xi is chosen normal to the plane formed by zi and zi − 1. The positive direction of xi is arbitrary. Then we choose the origin  at the point of intersection of zi and zi − 1. Note that in this case the parameter ai will be zero.
at the point of intersection of zi and zi − 1. Note that in this case the parameter ai will be zero.
This constructive procedure works for frames 0, …, n − 1 in an n-link robot. To complete the construction it is necessary to specify frame n. The final coordinate system onxnynzn is commonly referred to as the end effector or tool frame (see Figure 3.5). The origin  is most often placed symmetrically between the fingers of the gripper. The unit vectors along the xn, yn, and zn axes are labeled as n, s, and a, respectively. The terminology arises from the fact that the direction a is the approach direction, in the sense that the gripper typically approaches an object along the a direction. Similarly the s direction is the sliding direction, the direction along which the fingers of the gripper slide to open and close, and n is the direction normal to the plane formed by a and s.
is most often placed symmetrically between the fingers of the gripper. The unit vectors along the xn, yn, and zn axes are labeled as n, s, and a, respectively. The terminology arises from the fact that the direction a is the approach direction, in the sense that the gripper typically approaches an object along the a direction. Similarly the s direction is the sliding direction, the direction along which the fingers of the gripper slide to open and close, and n is the direction normal to the plane formed by a and s.

Figure 3.5 Tool frame assignment.
In most contemporary robots the final joint motion is a rotation of the end effector by θn and the final two joint axes, zn − 1 and zn, coincide. In this case, the transformation between the final two coordinate frames is a translation along zn − 1 by a distance dn followed (or preceded) by a rotation of θn about zn − 1. This is an important observation that will simplify the computation of the inverse kinematics in the next section.
Finally, note the following important fact. In all cases, whether the joint in question is revolute or prismatic, the quantities ai and αi are always constant for all i and are characteristic of the manipulator. If joint i is prismatic, then θi is also a constant, while di is the ith joint variable. Similarly, if joint i is revolute, then di is constant and θi is the ith joint variable.
Summary of the DH Procedure
We may summarize the procedure based on the DH convention in the following algorithm for deriving the forward kinematics for any manipulator.
- Step l: Locate and label the joint axes z0, …, zn − 1.
- Step 2: Establish the base frame. Set the origin anywhere on the z0-axis. The x0 and y0 axes are chosen conveniently to form a right-handed frame.
- For i = 1, …, n − 1 perform Steps 3 to 5.
-
Step 3:
Locate the origin
 where the common normal to zi and zi − 1 intersects zi. If zi intersects zi − 1 locate
where the common normal to zi and zi − 1 intersects zi. If zi intersects zi − 1 locate  at this intersection. If zi and zi − 1 are parallel, locate
at this intersection. If zi and zi − 1 are parallel, locate  in any convenient position along zi.
in any convenient position along zi. -
Step 4:
Establish xi along the common normal between zi − 1 and zi through
 , or in the direction normal to the zi − 1 − zi plane if zi − 1 and zi intersect.
, or in the direction normal to the zi − 1 − zi plane if zi − 1 and zi intersect. - Step 5: Establish yi to complete a right-handed frame.
-
Step 6:
Establish the end-effector frame onxnynzn. Assuming the nth joint is revolute, set zn = a parallel to zn − 1. Establish the origin
 conveniently along zn, preferably at the center of the gripper or at the tip of any tool that the manipulator may be carrying. Set yn = s in the direction of the gripper closure and set xn = n as s × a. If the tool is not a simple gripper set xn and yn conveniently to form a right-handed frame.
conveniently along zn, preferably at the center of the gripper or at the tip of any tool that the manipulator may be carrying. Set yn = s in the direction of the gripper closure and set xn = n as s × a. If the tool is not a simple gripper set xn and yn conveniently to form a right-handed frame. - Step 7:
Create a table of DH parameters ai, di, αi, θi.
-
ai = distance along xi from the intersection of the xi and zi − 1 axes to
 .
. -
di = distance along zi − 1 from
 to the intersection of the xi and zi − 1 axes. If joint i is prismatic, di is variable.
to the intersection of the xi and zi − 1 axes. If joint i is prismatic, di is variable. - αi = the angle from zi − 1 to zi measured about xi.
- θi = the angle from xi − 1 to xi measured about zi − 1. If joint i is revolute, θi is variable.
-
ai = distance along xi from the intersection of the xi and zi − 1 axes to
- Step 8: Form the homogeneous transformation matrices Ai by substituting the above parameters into Equation (3.10).
-
Step 9:
Form
 . This then gives the position and orientation of the tool frame expressed in base coordinates.
. This then gives the position and orientation of the tool frame expressed in base coordinates.
3.3 Examples
In the DH convention the only variable angle is θ, so we simplify notation by writing ci for cos θi, etc. We also denote θ1 + θ2 by θ12, and cos (θ1 + θ2) by c12, and so on. In the following examples it is important to remember that the DH convention, while systematic, still allows considerable freedom in the choice of some of the manipulator parameters. This is particularly true in the case of parallel joint axes or when prismatic joints are involved.
3.3.1 Planar Elbow Manipulator
Consider the two-link planar arm of Figure 3.6. The joint axes z0 and z1 are normal to the page. We establish the base frame o0x0y0z0 as shown by choosing the origin at the point of intersection of the z0 axis with the page and choosing the x0 axis in the horizontal direction. Note that the direction of the x0 is arbitrary. Once the base frame is established, the o1x1y1z1 frame is fixed as shown by the DH convention, where the origin  has been located at the intersection of z1 and the page. The final frame o2x2y2z2 is fixed by choosing the origin
has been located at the intersection of z1 and the page. The final frame o2x2y2z2 is fixed by choosing the origin  at the end of link 2 as shown. The DH parameters are shown in Table 3.1.
at the end of link 2 as shown. The DH parameters are shown in Table 3.1.

Figure 3.6 Two-link planar manipulator. The z-axes all point out of the page, and are not shown in the figure.
Table 3.1 DH parameters for 2-link planar manipulator. θ1 and θ2 are the joint variables.
| Link | ai | αi | di | θi |
| 1 | a1 | 0 | 0 | θ1 |
| 2 | a2 | 0 | 0 | θ2 |
The A matrices are determined from Equation (3.10) as
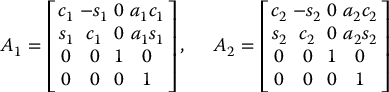
The T matrices are thus given by
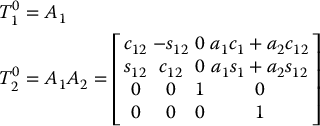
Notice that the first two entries of the last column of  are the x and y components of the origin
are the x and y components of the origin  in the base frame; that is,
in the base frame; that is,
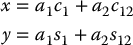
are the coordinates of the end effector in the base frame. The rotational part of  gives the orientation of the frame o2x2y2z2 relative to the base frame.
gives the orientation of the frame o2x2y2z2 relative to the base frame.
3.3.2 Three-Link Cylindrical Robot
Consider now the three-link cylindrical robot represented symbolically by Figure 3.7. We establish  as shown at joint 1. Note that the placement of the origin
as shown at joint 1. Note that the placement of the origin  along z0 and the direction of the x0 axis are arbitrary. Our choice of
along z0 and the direction of the x0 axis are arbitrary. Our choice of  is the most natural, but
is the most natural, but  could just as well be placed at joint 1. Next, since z0 and z1 coincide, the origin
could just as well be placed at joint 1. Next, since z0 and z1 coincide, the origin  is chosen at joint 1 as shown. The x1 axis is parallel to x0 when θ1 = 0 but, of course its direction will change since θ1 is variable. Since z2 and z1 intersect, the origin
is chosen at joint 1 as shown. The x1 axis is parallel to x0 when θ1 = 0 but, of course its direction will change since θ1 is variable. Since z2 and z1 intersect, the origin  is placed at this intersection. The direction of x2 is chosen parallel to x1 so that θ2 is zero. Finally, the third frame is chosen at the end of link 3 as shown.
is placed at this intersection. The direction of x2 is chosen parallel to x1 so that θ2 is zero. Finally, the third frame is chosen at the end of link 3 as shown.

Figure 3.7 Three-link cylindrical manipulator.
The DH parameters are shown in Table 3.2. The corresponding A and T matrices are
Table 3.2 DH parameters for 3-link cylindrical manipulator. θ1, d2, and d3 are the joint variables.
| Link | ai | αi | di | θi |
| 1 | 0 | 0 | d1 | θ1 |
| 2 | 0 | − 90 | d2 | 0 |
| 3 | 0 | 0 | d3 | 0 |
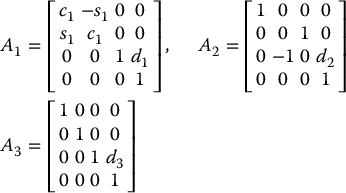
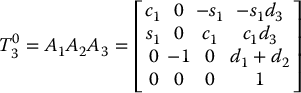
3.3.3 The Spherical Wrist
Figure 3.8 shows the spherical wrist, a three-link wrist mechanism for which the joint axes z3, z4, z5 intersect at  . The point
. The point  is called the wrist center. The DH parameters are shown in Table 3.3. The Stanford Manipulator is an example of a manipulator that possesses a wrist of this type.
is called the wrist center. The DH parameters are shown in Table 3.3. The Stanford Manipulator is an example of a manipulator that possesses a wrist of this type.

Figure 3.8 The spherical wrist frame assignment.
Table 3.3 DH parameters for the spherical wrist.
| Link | ai | αi | di | θi |
| 4 | 0 | − 90 | 0 | θ4 |
| 5 | 0 | 90 | 0 | θ5 |
| 6 | 0 | 0 | d6 | θ6 |
We show now that the final three joint variables, θ4, θ5, θ6 are a set of Euler angles ϕ, θ, and ψ, with respect to the coordinate frame o3x3y3z3. To see this we need only compute the matrices A4, A5, and A6 using Table 3.3 and Equation (3.10). This gives
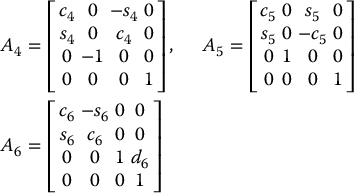
Multiplying these together yields
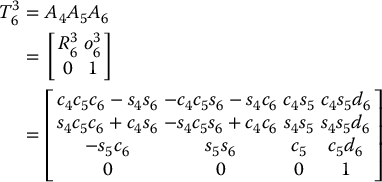
Comparing the rotational part  of
of  with the Euler angle transformation in Equation (2.27) shows that θ4, θ5, θ6 can indeed be identified as the Euler angles ϕ, θ, and ψ with respect to the coordinate frame o3x3y3z3.
with the Euler angle transformation in Equation (2.27) shows that θ4, θ5, θ6 can indeed be identified as the Euler angles ϕ, θ, and ψ with respect to the coordinate frame o3x3y3z3.
3.3.4 Cylindrical Manipulator with Spherical Wrist
Suppose that we now attach a spherical wrist to the cylindrical manipulator of Example 3.3.2 as shown in Figure 3.9. Note that the axis of rotation of joint 4 is parallel to z2 and thus coincides with the axis z3 of Example 3.3.2.) The implication of this is that we can immediately combine Equations (3.14) and (3.15) to derive the forward kinematic equations as
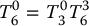
with  given by Equation (3.14) and
given by Equation (3.14) and  given by Equation (3.15). Therefore, the forward kinematic equations of this manipulator are given by
given by Equation (3.15). Therefore, the forward kinematic equations of this manipulator are given by
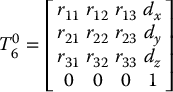
in which
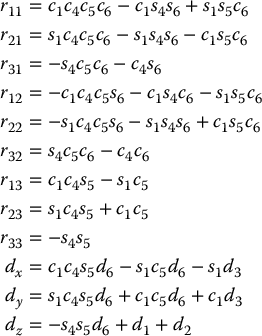
Notice how most of the complexity of the forward kinematics for this manipulator results from the orientation of the end effector while the expression for the arm position from Equation (3.14) is fairly simple. The spherical wrist assumption not only simplifies the derivation of the forward kinematics here, but will also greatly simplify the inverse kinematics problem in Chapter 5.

Figure 3.9 Cylindrical robot with spherical wrist.
3.3.5 Stanford Manipulator
Consider now the Stanford Manipulator shown in Figure 3.10. This manipulator is an example of a spherical (RRP) manipulator with a spherical wrist. This manipulator has an offset in the shoulder joint that slightly complicates both the forward and inverse kinematics problems.

Figure 3.10 DH coordinate frame assignment for the Stanford manipulator.
We first establish the joint coordinate frames using the DH convention. The DH parameters are shown in Table 3.4.
Table 3.4 DH parameters for the Stanford Manipulator. θi, i = 1, 2, 4, 5, 6 and d3 are variable.
| Link | di | ai | αi | θi |
| 1 | 0 | 0 | − 90 | θ1 |
| 2 | d2 | 0 | + 90 | θ2 |
| 3 | d3 | 0 | 0 | 0 |
| 4 | 0 | 0 | − 90 | θ4 |
| 5 | 0 | 0 | + 90 | θ5 |
| 6 | d6 | 0 | 0 | θ6 |
It is straightforward to compute the matrices Ai as
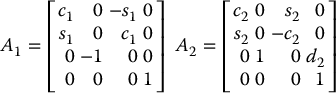
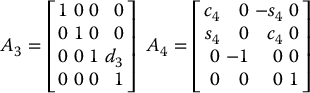

 is then given as
is then given as
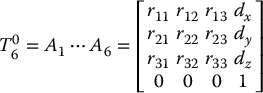
in which
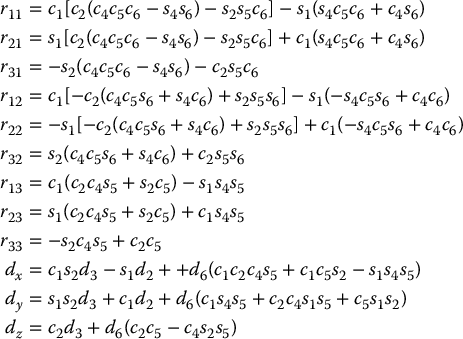
3.3.6 SCARA Manipulator
As another example of the general procedure, consider the SCARA manipulator of Figure 3.11. This manipulator consists of an RRP arm and a one degree-of-freedom wrist, whose motion is a roll about the vertical axis. The first step is to locate and label the joint axes as shown. Since all joint axes are parallel, we have some freedom in the placement of the origins. The origins are placed as shown for convenience. We establish the x0 axis in the plane of the page as shown. This choice is completely arbitrary, but it does determine the home position of the manipulator, which is defined relative to the zero configuration of the manipulator, that is, the position of the manipulator when the joint variables are equal to zero. The DH parameters are given in Table 3.5 and the A matrices are as follows.

Figure 3.11 DH coordinate frame assignment for the SCARA manipulator.
Table 3.5 DH parameters for the SCARA manipulator. θ1, i = 1, 2, 4 and d3 are variable.
| Link | ai | αi | di | θi |
| 1 | a1 | 0 | 0 | θ1 |
| 2 | a2 | 180 | 0 | θ2 |
| 3 | 0 | 0 | d3 | 0 |
| 4 | 0 | 0 | d4 | θ4 |
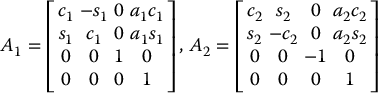
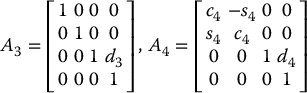
The forward kinematic equations are therefore given by
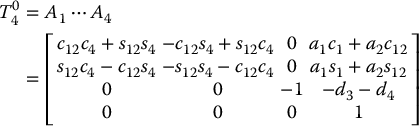
3.4 Chapter Summary
In this chapter we studied the relationships between joint variables qi and the position and orientation of the end effector for a general serial-link manipulator. We began by introducing the Denavit–Hartenberg convention for assigning coordinate frames to the links of a serial manipulator. Using the DH convention, four parameters are associated to each link of the robot, namely, the link length, link twist, link offset, and joint angle. Once a table of DH parameters is generated, the forward kinematic equations are computed as a product of homogeneous transformations that relate successive DH coordinate frames. We also discussed the kinematics of the spherical wrist and showed that the wrist joint variables can be identified with a set of Euler angles relating end-effector frame and a frame attached to the wrist center, i.e., the point where the spherical wrist joint axes intersect.
Problems
- Consider the three-link planar manipulator shown in Figure 3.12. Derive the forward kinematic equations using the DH convention.
- Consider the two-link Cartesian manipulator of Figure 3.13. Derive the forward kinematic equations using the DH convention.
- Consider the two-link manipulator of Figure 3.14, which has joint 1 revolute and joint 2 prismatic. Derive the forward kinematic equations using the DH convention.
- Consider the three-link planar manipulator of Figure 3.15. Derive the forward kinematic equations using the DH convention.
- Consider the three-link articulated robot of Figure 3.16. Derive the forward kinematic equations using the DH convention.
- Consider the three-link Cartesian manipulator of Figure 3.17. Derive the forward kinematic equations using the DH convention.
- Attach a spherical wrist to the three-link articulated manipulator of Problem 3–5 as shown in Figure 3.18. Derive the forward kinematic equations for this manipulator.
- Attach a spherical wrist to the three-link Cartesian manipulator of Problem 3–6 as shown in Figure 3.19. Derive the forward kinematic equations for this manipulator.
- Consider the PUMA 260 manipulator shown in Figure 3.20. Derive the complete set of forward kinematic equations by establishing appropriate DH coordinate frames, constructing a table of DH parameters, forming the A matrices, etc.

Figure 3.12 Three-link planar arm of Problem 3–1.

Figure 3.13 Two-link Cartesian robot of Problem 3–2.

Figure 3.14 Two-link planar arm of Problem 3–3.

Figure 3.15 Three-link planar arm with prismatic joint of Problem 3–4.

Figure 3.16 Three-link articulated robot.

Figure 3.17 Three-link Cartesian robot.

Figure 3.18 Elbow manipulator with spherical wrist.

Figure 3.19 Cartesian manipulator with spherical wrist.

Figure 3.20 PUMA 260 manipulator.
Notes and References
The Denavit–Hartenberg convention for assigning coordinate frames was first described in [35] and [70]. Since then, many articles and books have been written on the topics of kinematics of robots and general mechanisms, including [25], [37], [135], [16], and [181].
An alternative method to the DH convention to derive the forward kinematics of robots is based on the so-called product of exponentials. [118, 105] This method uses the fact that any rigid body motion (rotation and translation) may be represented as a so-called screw motion, which is a rotation about a fixed axis in space using the exponential coordinates defined in Chapter 2. Homogeneous transformations are then given as (matrix) exponentials. The reader may consult these texts for details.