Appendix E
CAMERA CALIBRATION

As described in Section 11.2, a digital image is a discrete array of gray level values. The objective of camera calibration is to determine all of the parameters that are necessary to relate the pixel coordinates (r, c) to the world coordinates (x, y, z) of a point in the camera’s field of view. In other words, given the coordinates of a point P relative to the world coordinate frame, after we have calibrated the camera we will be able to compute (r, c), the image pixel coordinates for the projection of this point.

Camera calibration is a ubiquitous problem in computer vision. Numerous solution methods have been developed, many of which have been implemented in open-source software libraries (e.g., OpenCV [17] and Matlab’s Computer Vision Toolbox [26]). Here, we present an approach that is conceptually straightforward and relatively easy to implement.

E.1 The Image Plane and the Sensor Array

In order to relate digital images to the 3D world, we must first determine the relationship between the image-plane coordinates (u, v) and the pixel coordinates (r, c). We typically define the origin of the pixel array to be located at a corner of the image rather than at the center of the image. Let the pixel array coordinates of the pixel that contains the principal point be given by (o_r, o_c). In general, the sensing elements in the camera will not be of unit size, nor will they necessarily be square. Denote by s_x and s_y the horizontal and vertical dimensions, respectively, of a pixel. Finally, it is often the case that the horizontal and vertical axes of the pixel array coordinate system point in opposite directions from the horizontal and vertical axes of the camera coordinate frame.¹ Combining these, we obtain the following relationship between image-plane coordinates and pixel array coordinates

(E.1)

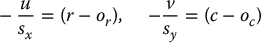
Note that the coordinates (r, c) will be integers, since they are the discrete indices into an array that is stored in computer memory. Therefore, this relationship is only an approximation. In practice, the value of (r, c) can be obtained by truncating or rounding the ratio on the left-hand side of these equations.

E.2 Extrinsic Camera Parameters

In Section 11.2.1, we considered only the case in which coordinates are expressed relative to the camera frame. In typical robotics applications, tasks are expressed in terms of the world coordinate frame. If we know the position and orientation of the camera frame relative to the world coordinate frame (i.e., if we know and , respectively), we can write

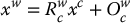
or, if we know and wish to solve for ,

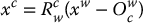
In the remainder of this section, to simplify notation, we will define

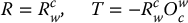
and we write

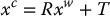
Together, R and T are called the extrinsic camera parameters.

Cameras are typically mounted on tripods or on mechanical positioning units. In the latter case, a popular configuration is the pan/tilt head. A pan/tilt head has two degrees of freedom: a rotation about the world z-axis and a rotation about the pan/tilt head’s x-axis. These two degrees of freedom are analogous to those of a human head, which can easily look up or down, and can turn from side to side. In this case, the rotation matrix is given by

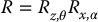
where θ is the pan angle and α is the tilt angle. More precisely, θ is the angle between the world x-axis and the camera x-axis, about the world z-axis, while α is the angle between the world z-axis and the camera z-axis, about the camera x-axis.

E.3 Intrinsic Camera Parameters

The mapping from 3D world coordinates to pixel coordinates is obtained by combining Equations (11.4) and (E.1) to obtain

(E.2)

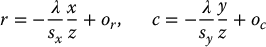
Thus, once we know the values of the parameters λ, s_x, o_r, s_y, o_c we can determine (r, c) from (x, y, z), where (x, y, z) are coordinates relative to the camera frame. In fact, we don’t need to know all of λ, s_x, s_y; it is sufficient to know the ratios

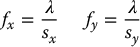
These parameters f_x, o_r, f_y, o_c are known as the intrinsic camera parameters. They are constant for a given camera and do not change when the camera moves.

E.4 Determining the Camera Parameters

Of all the camera parameters, o_r, o_c (the image pixel coordinates of the principal point) are the easiest to determine. This can be done by using the idea of vanishing points, which was introduced in Example 11.2. The vanishing points for three mutually orthogonal sets of parallel lines in the world will define a triangle in the image. The orthocenter of this triangle (that is, the point at which the three altitudes intersect) is the image principal point. Thus, a simple way to compute the principal point is to position a cube in the workspace, find the edges of the cube in the image (this will produce the three sets of mutually orthogonal parallel lines), compute the intersections of the image lines that correspond to each set of parallel lines in the world (this will produce three points in the image), and determine the orthocenter for the resulting triangle.

To determine the remaining camera parameters, we construct a system of equations in terms of the known coordinates of points in the world and the pixel coordinates of their projections in the image. The unknowns in this system are the camera parameters. The first step is to acquire a data set of the form {r_i, c_i, x_i, y_i, z_i} for i = 1⋅⋅⋅N, in which r_i, c_i are the image pixel coordinates of the projection of a point in the world with coordinates x_i, y_i, z_i relative to the world coordinate frame. This acquisition is often done manually, for example, by placing a small bright light at known (x, y, z) coordinates in the world and then hand selecting the corresponding image point.

Once we have acquired the data set, we proceed to set up a linear system of equations. The extrinsic parameters of the camera are given by

With respect to the camera frame, the coordinates of a point in the world are thus given by

Combining these three equations with Equation (E.2) we obtain

(E.3)

(E.4)

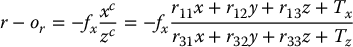
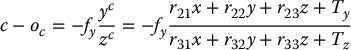
Since we know the coordinates of the principal point, we can simplify these equations by using the coordinate transformation

We now write the two transformed projection equations as functions of the unknown variables r_ij, T_x, T_y, T_z, f_x, f_y. This is done by solving Equations (E.3) and (E.4) for z^c, and setting the resulting equations to be equal to one another. In particular, r_i, c_i, x_i, y_i, z_i we have

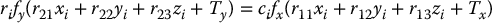
Defining α = f_x/f_y, we can rewrite this as

We can combine the N such equations into the matrix equation

(E.5)

in which

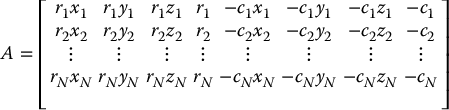
and

If is a solution for Equation (E.5) we only know that this solution is some scalar multiple of the desired solution x, namely,

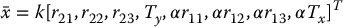
in which k is an unknown scale factor. In order to solve for the true values of the camera parameters, we can exploit constraints that arise from the fact that is a rotation matrix. In particular,

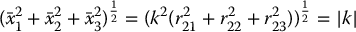
and likewise

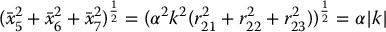
Note that by definition, α > 0.

Our next task is to determine the sign of k. Using Equation (E.2) we see that rx^c < 0 (recall that we have used the coordinate transformation r ← r − o_r). Therefore, we choose k such that r(r₁₁x + r₁₂y + r₁₃z + T_x) < 0.

At this point we know the values for k, α, r₂₁, r₂₂, r₂₃, r₁₁, r₁₂, r₁₃, T_x, T_y, and all that remains is to determine T_z, f_x, f_y, since the third column of R can be determined as the vector cross product of its first two columns. Since α = f_x/f_y, we need only determine T_z and f_x. Returning again to the projection equations, we can write

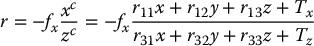
Using an approach similar to that used above to solve for the first eight parameters, we can write this as the linear system

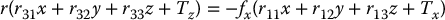
which can easily be solved for T_z and f_x.