Appendix D
OPTIMIZATION
In this Appendix we present some terminology and results from optimization theory that are used in the text. We will state the various results without proof. The reader should consult any introductory textbook on optimization for details.
A general optimization problem may be stated as follows:
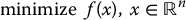
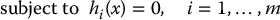
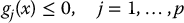
The function  is called the objective function or cost function. The functions
is called the objective function or cost function. The functions  and
and  are equality and inequality constraints, respectively.
are equality and inequality constraints, respectively.
A vector  is called a feasible point if it satisfies the constraints. For
is called a feasible point if it satisfies the constraints. For  , if gj(x) = 0, the constraint gj is called an active constraint, while, if gj(x) < 0, the constraint is called inactive. The equality constraints hi = 0 are, therefore, considered always active.
, if gj(x) = 0, the constraint gj is called an active constraint, while, if gj(x) < 0, the constraint is called inactive. The equality constraints hi = 0 are, therefore, considered always active.
D.1 Unconstrained Optimization
In the case that there are no constraints on the objective function f(x) we may give simple conditions for local optimality. For the problem
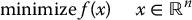
an extreme point or extremum of f(x) is a vector x* satisfying
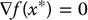
A necessary condition for a vector  to be a local minimizer of f(x) is that x* be a extremum of f(x).
to be a local minimizer of f(x) is that x* be a extremum of f(x).
If x* is an extremum of f(x) then a sufficient condition for x* to be a local minimizer of f(x) is that the Hessian matrix of f(x) is positive definite at x = x*.
Gradient Descent
Since the gradient of a scalar function points in the direction of maximum increase of the function, a common approach to find the minimum value of an unconstrained objective function f(x) is to choose an initial guess x0 for the value of x* and compute iteratively a sequence of vectors x1, x2, …, such that
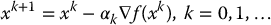
In other words, xk + 1 points in the direction of the negative gradient of f at the value xk. The scalar αk is called the step size and influences the rate of convergence of the sequence to the minimizer x*. This is known as the method of Gradient Descent. The method of Steepest Descent is a gradient descent method where the step size αk is chosen at each iterative k according to
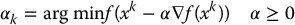
In other problems, such as the artificial potential field approach for motion planning considered in Chapter 7, the step size may be taken as a small constant value to avoid the case where a trajectory contacts an obstacle.
D.2 Constrained Optimization
In the case that there are no inequality constraints we have
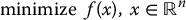
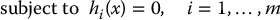
A vector x* satisfying the constraints hi(x*) = 0 is called a regular point if the gradient vectors ∇h1(x*), …, ∇hm(x*) are linearly independent at x*.
Lagrange Multipliers
Define the Lagrangian function
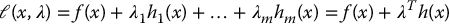
where the λ = (λ1, …, λm) is a vector of Lagrange multipliers. The following theorem, known as Lagrange’s theorem, gives a necessary condition for a solution to the above minimization problem.
Theorem D.1
Let x* be a regular point of the optimization problem (D.5)-(D.6). If x* is a minimizer of  subject to the constraints hi(x) = 0, i = 1, …, m, then there is a vector λ* = [λ*1, …, λm*] such that
subject to the constraints hi(x) = 0, i = 1, …, m, then there is a vector λ* = [λ*1, …, λm*] such that
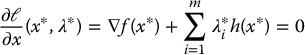
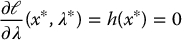
Lagrange’s theorem says that, at a local minimum x*, the gradient of the objective function can be expressed as a linear combination of the equality constraints.
Next, define the matrix function
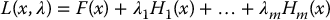
Where F(x) and Hi(x) are the Hessian matrices of f(x) and hi(x), respectively. Then, if x*, λ* satisfy Equations (D.7) and (D.8), a sufficient condition for x* to be a strict local minimum is that the matrix L(x*, λ*) is positive definite.
Example D.1
Consider the problem
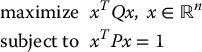
where Q and P are n × n symmetric positive definite matrices. We first note that maximizing an objective f(x) is equivalent to minimizing − f(x). Therefore, we form the Lagrangian function
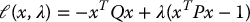
The necessary conditions for optimality are then
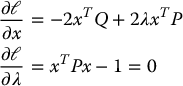
Any feasible point for this problem is regular. From the first equation above we have
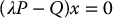
which, since P is symmetric and positive definite, can be written as
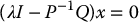
Therefore, a solution (x*, λ*), if it exists, is such that x* is an eigenvector of P− 1Q with λ* the corresponding eigenvector.