Appendix C
LYAPUNOV STABILITY
We give here some basic results on stability theory for nonlinear systems. For simplicity we treat only time-invariant systems. For a more general treatment of the subject the reader is referred to [180]. We first need a few definitions from real analysis regarding continuity and differentiability of functions.
C.1 Continuity and Differentiability
Definition C.1 (Continuous function).
Let  be an open subset of
be an open subset of  . A function
. A function  is continuous at a point
is continuous at a point  if, for all ε > 0, there exists a δ > 0 such that, if |x − x0| < δ (and
if, for all ε > 0, there exists a δ > 0 such that, if |x − x0| < δ (and  ), then |f(x) − f(x0)| < ε.
), then |f(x) − f(x0)| < ε.
An alternative characterization of continuity is that  is continuous at x = x0 if f(x) → f(x0) as x → x0.
is continuous at x = x0 if f(x) → f(x0) as x → x0.
Definition C.2 (Uniform continuity).
A function  is uniformly continuous on
is uniformly continuous on  if for every ε > 0 there exists a δ > 0 such that |x − y| < δ implies |f(x) − f(y)| < ε.
if for every ε > 0 there exists a δ > 0 such that |x − y| < δ implies |f(x) − f(y)| < ε.
Continuity of a function is a property that holds at a point. Uniform continuity, on the other hand, is a global property on  .
.
Definition C.3 (Derivative).
A function  is differentiable at
is differentiable at  if
if
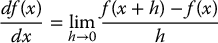
exists and is finite.
A function of several variables,  , where
, where  , is differentiable if the partial derivatives exist and are finite, where the partial derivatives are defined for k = 1, …, n as
, is differentiable if the partial derivatives exist and are finite, where the partial derivatives are defined for k = 1, …, n as
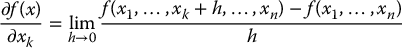
We say that a function is continuously differentiable if the derivative function exists and is continuous.
Since the derivative  is itself a function, we can ask if the derivative function is continuous, differentiable, and so on. Higher derivatives are denoted as
is itself a function, we can ask if the derivative function is continuous, differentiable, and so on. Higher derivatives are denoted as  for functions of a single variable.
for functions of a single variable.
For partial derivatives, the order in which higher derivatives are computed is important. For example, if f is a function of 3-variables, we may compute a second partial derivative with respect to any of the variables, in any order, i.e.
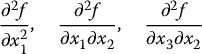
and so on. These are called mixed partials. Note that equality of the mixed partials, such as,
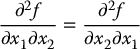
is true if the derivatives themselves are continuous, i.e. if f is at least twice continuously differentiable.
In order not to have to specify the precise continuity properties of a function each time we use it, we will often use the term smooth function to mean a function that is continuously differentiable as many times as needed in a particular context.
Gradient, Hessian, and Jacobian
Given a smooth scalar function  , we define the differential of f, denoted by df, as
, we define the differential of f, denoted by df, as
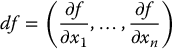
The vector function
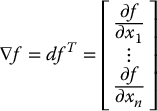
is called the gradient of f. The gradient of a scalar function is orthogonal to the level curves of the function and points in the direction of maximum increase of the function.
The n × n matrix of second derivatives of the function f
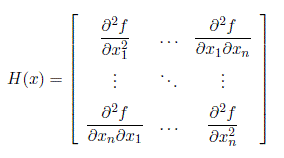
is called the Hessian of f. The Hessian matrix is symmetric if the entries are continuous and describes the local curvature of the function f.
Let  be a smooth function from
be a smooth function from  to
to  . The m × n matrix
. The m × n matrix
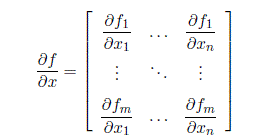
is called the Jacobian of f. We also use the notation J(x) to mean a Jacobian.
C.2 Vector Fields and Equilibria
Definition C.4 (Vector Field).
A vector field f on  is a smooth function
is a smooth function  . A vector field f is linear if f(x) = Ax, where A is an n × n matrix of real numbers.
. A vector field f is linear if f(x) = Ax, where A is an n × n matrix of real numbers.
We can think of a differential equation
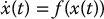
as being defined by a vector field f on  . A solution or trajectory t → x(t) of Equation (C.1), with x(t0) = x0, is then a curve C in
. A solution or trajectory t → x(t) of Equation (C.1), with x(t0) = x0, is then a curve C in  , beginning at x0, parameterized by t, such that, at each point of C, the vector field f(x(t)) is tangent to C.
, beginning at x0, parameterized by t, such that, at each point of C, the vector field f(x(t)) is tangent to C.  is then called the state space of the system given by Equation (C.1).
is then called the state space of the system given by Equation (C.1).
Definition C.5 (Equilibrium Point).
A vector  is an equilibrium point or fixed point for the system (C.1) if and only if f(x*) = 0. For autonomous, or time-invariant vector fields we may take x* = 0 without loss of generality.
is an equilibrium point or fixed point for the system (C.1) if and only if f(x*) = 0. For autonomous, or time-invariant vector fields we may take x* = 0 without loss of generality.
If x(t0) = x* is an equilibrium point for (C.1), then the function x(t) ≡ x* for t > t0 is a solution of Equation (C.1), called the null or equilibrium solution. In other words, if the system represented by Equation (C.1) starts initially at an equilibrium, then it remains at the equilibrium thereafter.
The question of stability deals with the solutions of Equation (C.1) for initial conditions away from the equilibrium point. Intuitively, the null solution should be called stable if, for initial conditions close to the equilibrium, the solution remains close thereafter. We can formalize this notion into the following.
Definition C.6.
Given the nonlinear system defined by Equation (C.1), suppose that  is an equilibrium. Then the null solution x(t) = 0 is said to be
is an equilibrium. Then the null solution x(t) = 0 is said to be
- stable if and only if, for any ε > 0 there exist δ = δ(ε) > 0 such that
(C.2)
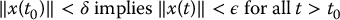
- asymptotically stable if x = 0 is stable and, in addition,
(C.3)
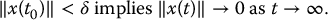
- unstable if it is not stable.
The stability, respectively, asymptotic stability, is said to be global if the corresponding conditions hold for every initial condition  .
.
This situation is illustrated by Figure C.1 and says that the system is stable if the solution remains within a ball of radius ε around the equilibrium, provided that the initial condition lies in a ball of radius δ around the equilibrium. To put it another way, a system is stable if “small” perturbations in the initial conditions result in “small” perturbations from the null solution.

Figure C.1: Illustrating the definition of stability.
If the equilibrium is asymptotically stable, then the solutions return to the equilibrium as t → ∞. If the equilibrium is unstable, then, given ε > 0, there is no value of δ satisfying (C.3).
The above notions of stability are local in nature, that is, they may hold for initial conditions “sufficiently near” the equilibrium point but may fail for initial conditions farther away from the equilibrium. Stability (respectively, asymptotic stability) is said to be global if it holds for all initial conditions. A stronger notion than asymptotic stability is that of exponential stability defined next.
Definition C.7 (Exponential Stability).
The equilibrium x = 0 of the system Equation (C.1) is exponentially stable if there are positive constants α and γ such that
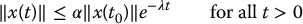
The exponential stability is local or global depending on whether or not the inequality (C.4) holds for all initial conditions  .
.
For a linear system
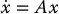
the null solution is globally exponentially stable if and only if all eigenvalues of the matrix A lie in the open left half of the complex plane. Such a matrix is called a Hurwitz matrix. For nonlinear systems, global stability cannot be so easily determined. However, local stability of the null solution of a nonlinear system  can sometimes be determined by examining the eigenvalues of the Jacobian of the vector field f(x).
can sometimes be determined by examining the eigenvalues of the Jacobian of the vector field f(x).
Given the system (C.1) and suppose x = 0 is an equilibrium point. Let A be the n × n Jacobian matrix of f(x), evaluated at x = 0. In other words

The system
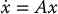
is called the linear approximation about the equilibrium of the nonlinear system (C.1).
Theorem C.1
- Suppose A in (C.5) is a Hurwitz matrix so that x = 0 is a globally exponentially stable equilibrium point for the linearized system. Then x = 0 is locally exponentially stable for the nonlinear system (C.1).
- Suppose A has one or more eigenvalues in the open right half plane so that x = 0 is an unstable equilibrium point for the linear system (C.5). Then x = 0 is unstable for the nonlinear system (C.1).
- Suppose A has no eigenvalues in the open right half plane but one or more eigenvalues on the jω-axis. Then the stability properties of the equilibrium x = 0 for the nonlinear system (C.1) cannot be determined from A alone.
Eigenvalues on the jω-axis are called critical eigenvalues. Examining the eigenvalues of the linear approximation of a nonlinear system in order to determine its stability properties is referred to as Lyapunov’s indirect method. We see that local stability of the equilibrium of the nonlinear system (C.1) can be determined provided the matrix A of the linear approximation has no critical eigenvalues. If A has critical eigenvalues, or if one desires to determine the global stability properties of the nonlinear system (C.1) then Lyapunov’s indirect method is inconclusive and other methods must be used. Lyapunov’s direct method, also called the second method of Lyapunov introduced below, addresses these latter issues.
C.3 Lyapunov Functions
Definition C.8 (Positive Definite Functions).
Let  be a continuously differentiable scalar function, such that V(0) = 0 and V(x) > 0 for x > 0. Then V is said to be positive definite.
be a continuously differentiable scalar function, such that V(0) = 0 and V(x) > 0 for x > 0. Then V is said to be positive definite.
We say that V(x) is positive semi-definite or nonnegative definite if V(x) ⩾ 0 for all x and we say that V(x) is negative (semi-)definite if − V(x) is positive (semi-)definite.
A particularly useful class of positive definite functions are quadratic forms
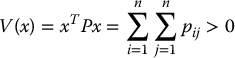
where P = (pij) is a symmetric positive definite matrix.
The level surfaces of a positive definite quadratic form, given as solutions of xTPx = constant, are ellipsoids in  . A positive definite quadratic form defines a norm on
. A positive definite quadratic form defines a norm on  . In fact, given the usual norm ‖x‖ on Rn, the function V given as
. In fact, given the usual norm ‖x‖ on Rn, the function V given as
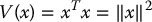
is a positive definite quadratic form corresponding to the choice P = I, the n × n identity matrix.
C.4 Stability Criteria
Definition C.9 (Lyapunov function candidate).
Let  be a continuously differentiable scalar function on
be a continuously differentiable scalar function on  . Furthermore, suppose that V is positive definite. Then V is called a Lyapunov function candidate.
. Furthermore, suppose that V is positive definite. Then V is called a Lyapunov function candidate.
The power of Lyapunov stability theory comes from the fact that any function may be used in an attempt to show stability of a given system provided it is a Lyapunov function candidate according to the above definition.
Definition C.10
By the derivative of V along trajectories of Equation (C.1), or the derivative of V in the direction of the vector field f(x) defining Equation (C.1), we mean
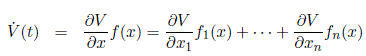
Suppose that we evaluate the Lyapunov function candidate V at points along a solution trajectory x(t) of Equation (C.1) and find that V(t) is decreasing for increasing t. Intuitively, since V acts like a norm, this must mean that the given solution trajectory is converging toward the origin. This is the idea of Lyapunov stability theory.
Theorem C.2
The null solution of Equation (C.1) is stable if there exists a Lyapunov function candidate V such that  is negative semi-definite along solution trajectories of Equation (C.1), that is, if
is negative semi-definite along solution trajectories of Equation (C.1), that is, if
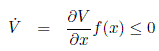
The inequality (C.6) says that the derivative of V computed along solutions of Equation (C.1) is nonpositive, which says that V itself is nonincreasing along solutions. Since V is a measure of how far the solution is from the origin, (C.6) says that a solution starting sufficiently near the origin must remain near the origin. If a Lyapunov function candidate V can be found satisfying (C.6) then V is called a Lyapunov function for the system given by Equation (C.1).
Note that Theorem .23 gives only a sufficient condition for stability of Equation (C.1). If one is unable to find a Lyapunov function satisfying the inequality (C.6) it does not mean that the system is unstable. However, an easy sufficient condition for instability of Equation (C.1) is for there to exist a Lyapunov function candidate V such that  along at least one solution of the system.
along at least one solution of the system.
Theorem C.3
The null solution of Equation (C.1) is asymptotically stable if there exists a Lyapunov function candidate V such that  is strictly negative definite along solutions of Equation (C.1), that is,
is strictly negative definite along solutions of Equation (C.1), that is,
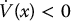
The strict inequality in Equation (C.7) means that V is actually decreasing along solution trajectories of Equation (C.1) and hence, the trajectories must be converging to the equilibrium point.
C.5 Global and Exponential Stability
The condition  along solution trajectories of a given system guarantees only local asymptotic stability even if the condition holds globally. In order to show global (asymptotic) stability, the Lyapunov function V must satisfy an additional condition, known as radial unboundedness.
along solution trajectories of a given system guarantees only local asymptotic stability even if the condition holds globally. In order to show global (asymptotic) stability, the Lyapunov function V must satisfy an additional condition, known as radial unboundedness.
Definition C.11.
Suppose  is a continuously differentiable function. V(x) is said to be radially unbounded if
is a continuously differentiable function. V(x) is said to be radially unbounded if
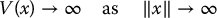
With this additional property for V we can state the following:
Theorem C.4.
Let  be Lyapunov function candidate for the system given by Equation (C.1) and suppose that V is radially unbounded. Then
be Lyapunov function candidate for the system given by Equation (C.1) and suppose that V is radially unbounded. Then  implies that x = 0 is globally asymptotically stable.
implies that x = 0 is globally asymptotically stable.
A sufficient condition for exponential stability is the following:
Theorem C.5.
Suppose that V is a Lyapunov function candidate for the system given by Equation (C.1) such that
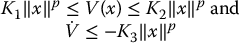
where K1, K2, K3, and p are positive constants. Then the origin x = 0 is exponentially stable. Moreover, if the inequalities (C.8) hold globally, then x = 0 is globally exponentially stable.
C.6 Stability of Linear Systems
Consider the linear system given by Equation (C.5) and let
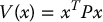
be a Lyapunov function candidate, where P is symmetric and positive definite. Computing  along solutions of Equation (C.5) yields
along solutions of Equation (C.5) yields
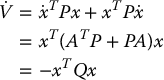
where we have defined Q as
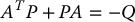
Theorem C.2 says that if Q given by Equation (C.10) is positive definite (it is automatically symmetric since P is symmetric), then the linear system given by Equation (C.5) is globally exponentially stable. One approach that we can take is to first fix Q to be symmetric, positive definite and solve Equation (C.10), which is called a matrix Lyapunov equation, for P. If a symmetric positive definite solution P can be found to this equation, then the matrix A in Equation (C.5) is Hurwitz and xTPx is a Lyapunov function for the linear system (C.5). The converse to this statement also holds. In fact, we can summarize these statements as
Theorem C.6.
Given an n × n matrix A, then all eigenvalues of A have negative real part if and only if for every symmetric positive definite n × n matrix Q, the matrix Lyapunov equation (C.10) has a unique positive definite solution P.
Thus, we can reduce the determination of stability of a linear system to the solution of a system of linear equations.
C.7 LaSalle’s Theorem
The main difficulty in the use of Lyapunov stability theory is finding a suitable Lyapunov function satisfying  in order to prove asymptotic stability. LaSalle’s invariance principle, or LaSalle’s theorem gives us a tool to determine the asymptotic properties of a system in the weaker case that V is only negative semidefinite, that is, when
in order to prove asymptotic stability. LaSalle’s invariance principle, or LaSalle’s theorem gives us a tool to determine the asymptotic properties of a system in the weaker case that V is only negative semidefinite, that is, when  .
.
The version of LaSalle’s Theorem here follows closely the development in [76]. Consider the nonlinear system
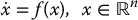
where f is a smooth vector field on  with f(0) = 0.
with f(0) = 0.
Definition C.12 (Invariant Set).
A set M is invariant or positively invariant, with respect to the system (C.11) if
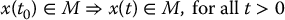
Theorem C.7 (LaSalle’s Theorem)
Let D be a region in  and let Ω⊂D be a compact set that is positively invariant with respect to the nonlinear system (C.11). Let
and let Ω⊂D be a compact set that is positively invariant with respect to the nonlinear system (C.11). Let  be a continuously differentiable function such that
be a continuously differentiable function such that  in Ω. Let E be the set of all points in Ω where
in Ω. Let E be the set of all points in Ω where  . Let M be the largest invariant set in E. Then every solution starting in Ω approaches M as t → ∞.
. Let M be the largest invariant set in E. Then every solution starting in Ω approaches M as t → ∞.
As a corollary to LaSalle’s Theorem it follows that the equilibrium solution x = 0 of Equation (C.11) is asymptotically stable if V does not vanish identically along any solution of Equation (C.11) other than the null solution, that is, if the only solution of Equation (C.11) satisfying  is the null solution.
is the null solution.
Note that, in the statement of LaSalle’s theorem, the function V need not be positive definite, i.e., it need not be a Lyapunov function. The key is to find a compact, positively invariant set Ω so that  in Ω. In the case that V is a valid Lyapunov function, then such a set Ω may be determined from the level sets of V. We state this as the following proposition, whose proof is immediate from the definition of a Lyapunov function.
in Ω. In the case that V is a valid Lyapunov function, then such a set Ω may be determined from the level sets of V. We state this as the following proposition, whose proof is immediate from the definition of a Lyapunov function.
Proposition C.1.
Let V be a Lyapunov function candidate and let V− 1(c0) be any level surface of V, that is,
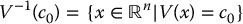
for some constant c0 > 0. If
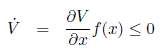
for x ∈ V− 1(c0). Then the set  is positively invariant for the system (C.1).
is positively invariant for the system (C.1).
C.8 Barbalat’s Lemma
LaSalle’s theorem is valid only for autonomous, or time-invariant, systems. The next result, known as Barbalat’s lemma, provides an additional tool for showing stability and asymptotic stability for nonlinear systems, including time-varying systems. Barbalat’s lemma will prove useful for analyzing the trajectory tracking performance of robust and adaptive nonlinear controllers.
Lemma C.1. (Barbalat)
If  is a square integrable function and
is a square integrable function and  is uniformly continuous, then
is uniformly continuous, then  as t → ∞.
as t → ∞.
Remark C.1
1: A function  is square integrable if
is square integrable if
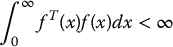
2: The statement that  is uniformly continuous can be replaced by the statement
is uniformly continuous can be replaced by the statement  is bounded.
is bounded.
Another important notion related to stability is the notion of uniform ultimate boundedness of solutions.
Definition C.13
A solution  for Equation (C.1) is said to be uniformly ultimately bounded (u.u.b.), with ultimate bound b if there exist positive constants a and b and a time T = T(a, b) such that
for Equation (C.1) is said to be uniformly ultimately bounded (u.u.b.), with ultimate bound b if there exist positive constants a and b and a time T = T(a, b) such that
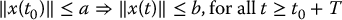
The ultimate boundedness is global if (C.12) hold for arbitrarily large a.
Uniform ultimate boundedness says that the solution trajectory of Equation (C.1) will ultimately enter the ball of radius b and remain there for t > t0 + T. If b defines a small region about the equilibrium, then uniform ultimate boundedness is a practical notion of stability that is useful in control system design.
Uniform ultimate boundedness is often established via Lyapunov theory as follows: Suppose V is a Lyapunov function candidate for the system (C.1) and suppose that the set Ωε = {0 ⩽ V(x) ⩽ ε} is compact. If  outside the set Ωε, then Ωε is positively invariant for (C.1) and, moreover, trajectories starting outside of Ωε will eventually enter and, therefore, remain in Ωε. Therefore, the system is uniformly ultimately bounded with bound
outside the set Ωε, then Ωε is positively invariant for (C.1) and, moreover, trajectories starting outside of Ωε will eventually enter and, therefore, remain in Ωε. Therefore, the system is uniformly ultimately bounded with bound  .
.