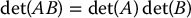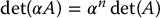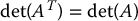Appendix B
LINEAR ALGEBRA
We assume that the reader has some familiarity with basic properties of vectors and matrices, such as matrix addition, multiplication, and determinants. For additional background, see [9, 60].
The symbol  denotes the set of real numbers and
denotes the set of real numbers and  denotes the set of n-tuples of real numbers. We use lower case letters a, b, c, x, y, etc., to denote scalars in
denotes the set of n-tuples of real numbers. We use lower case letters a, b, c, x, y, etc., to denote scalars in  and vectors in
and vectors in  . Uppercase letters A, B, C, M, R, etc., denote matrices.
. Uppercase letters A, B, C, M, R, etc., denote matrices.
B.1 Vectors
Vectors in  are defined as column vectors
are defined as column vectors
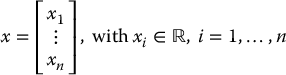
The entries x1, …, xn are called components or coordinates of x. The transpose of a vector x, denoted xT, is the row vector
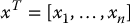
In this text we will often drop the superscript T when the vector x is not part of a displayed equation and simply write
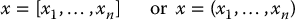
to denote x as a row instead of a column. This is done simply to improve the readability of the text where convenient and the reader should bear in mind that vectors are, by definition, columns. Also, since we do not use bold font or arrows to denote vectors, the difference between, for example, xi as a vector and xi as a component of a vector x should be clear from the context.
Linear Independence
A set of vectors {x1, …, xm} is said to be linearly independent if and only if, for arbitrary scalars  ,
,

Otherwise, the vectors x1, …, xm are said to be linearly dependent.
Remark B.1.
It is easy to show that a set of vectors x1, …, xm is linearly dependent if and only if some xk, for 2 ⩽ k ⩽ m, is a linear combination of the preceding vectors x1, …, xk − 1.
A basis of a real vector space is a linearly independent set of vectors {e1, …, em} such that every vector x can be written as a linear combination
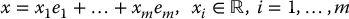
The coordinate representation x = (x1, …, xm) is uniquely determined by the particular basis {e1, …, em}. The dimension of the vector space is the number of vectors in any basis.
Subspaces
A set of vectors  contained in a vector space
contained in a vector space  is a subspace of
is a subspace of  if αx + βy belongs to
if αx + βy belongs to  for every x and y in
for every x and y in  and every α and β in
and every α and β in  . In other words
. In other words  is closed under the operations of addition and scalar multiplication. A subspace
is closed under the operations of addition and scalar multiplication. A subspace  is itself a vector space. The dimension of
is itself a vector space. The dimension of  is less than or equal to the dimension of
is less than or equal to the dimension of  .
.
B.2 Inner Product Spaces
An inner product in a (real) vector space is a scalar-valued, bilinear function < ·, · > of pairs of vectors x and y such that
- < x, y > = < y, x >
- < α1x + α2y, z > =α1 < x, z > +α2 < y, z > where a1 and a2 are scalars
- < x, x > ⩾ 0 and < x, x > = 0 if and only if x = 0
An inner product space is a vector space with an inner product. An inner product induces a norm ‖x‖ on an inner product space via the formula
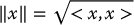
The norm generalizes the usual notion of length of a vector. Some useful properties of the inner product and norm include
Cauchy–Schwartz inequality: | < x, y > | ⩽ ‖x‖ ‖y‖ with equality if and only if x and y are linearly dependent.
homogeneity: ‖αx‖ = |α|‖x‖ for x a vector and α a scalar.
triangle inequality: ‖x + y‖ ⩽ ‖x‖ + ‖y‖
parallelogram law: ‖x + y‖2 + ‖x − y‖2 = 2‖x‖2 + 2‖y‖2
Euclidean Space
The Euclidean space  is an inner product space with inner product defined as
is an inner product space with inner product defined as
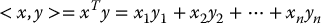
The inner product (B.1) on  is also denoted by x · y and called the dot product or scalar product. For vectors in
is also denoted by x · y and called the dot product or scalar product. For vectors in  or
or  the scalar product can be expressed as
the scalar product can be expressed as
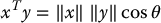
where θ is the angle between the vectors x and y.
We will use i, j, and k to denote the standard unit vectors in 
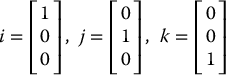
Using this notation, a vector x = (x1, x2, x3) may be written as
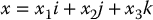
and the components of x are equal to the dot products
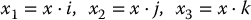
Orthogonal Complement
If W is a subspace of  , the orthogonal complement of W in
, the orthogonal complement of W in  is the subspace
is the subspace
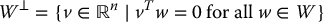
The symbol W⊥ is read “W perp”. Thus W⊥ is the set of all vectors  that are orthogonal to all vectors w ∈ W. The orthogonal complement of a subspace W in
that are orthogonal to all vectors w ∈ W. The orthogonal complement of a subspace W in  satisfies the following:
satisfies the following:
- W⊥ is also a subspace of
- (W⊥)⊥ = W
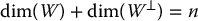
B.3 Matrices
Matrices and matrix representations of linear transformations are fundamental to most of the concepts in this text, from kinematics and dynamics, to control. A linear transformation A on a vector space  is a function
is a function  such that
such that
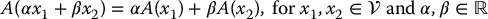
We will denote A(x) by Ax. We represent linear transformations in coordinate form as matrices by taking a particular basis for  .
.
An m × n matrix A = (aij) over  is an ordered array of real numbers with m row vectors (ai1, …, ain) for i = 1, …, m, and n column vectors (a1j, …, amj), for j = 1, …, n written as
is an ordered array of real numbers with m row vectors (ai1, …, ain) for i = 1, …, m, and n column vectors (a1j, …, amj), for j = 1, …, n written as
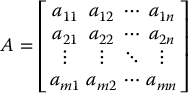
The matrix A is a representation of a linear transformation from  to
to  . If n = m, i.e., if the number of rows and the number of columns are equal, then the matrix A is said to be square. The set of n × n square matrices, which we denote by
. If n = m, i.e., if the number of rows and the number of columns are equal, then the matrix A is said to be square. The set of n × n square matrices, which we denote by  , is itself a vector space of dimension n2.
, is itself a vector space of dimension n2.
The rank of a matrix A is the largest number of linearly independent rows (or columns) of A. Thus, the rank of an m × n matrix can be no greater than the minimum of m and n.
The transpose of a matrix A is denoted AT and is formed by interchanging rows and columns of A.

Thus AT is an n × m matrix. Some properties of the matrix transpose are
- (AT)T = A
- (AB)T = BTAT
- (A + B)T = AT + BT
A square n × n matrix A is said to be
- symmetric if AT = A
- skew-symmetric if AT = −A
- orthogonal if ATA = AAT = I, where I is the n × n identity matrix
Matrix Trace
The trace of an n × n matrix A, denoted Tr(A) is the sum of the diagonal entries of A. Thus, if A = (aij), then Tr(A) = ∑ni = 1aii = a11 + ⋅⋅⋅ + ann.
The Determinant
A determinant is a function that assigns a particular scalar to a linear transformation (matrix)  . For our purposes we may define the determinant,
. For our purposes we may define the determinant,  , of a square matrix A via the recursive formula that holds for any i = 1, …, n
, of a square matrix A via the recursive formula that holds for any i = 1, …, n
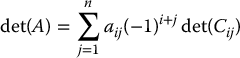
where Cij is the (n − 1) × (n − 1) matrix formed by deleting the i-th row and j-th column of A. The matrix determinant satisfies the following properties
If  , the matrix A is called singular; otherwise A is nonsingular or invertible. The inverse of a square matrix
, the matrix A is called singular; otherwise A is nonsingular or invertible. The inverse of a square matrix  is a matrix
is a matrix  satisfying
satisfying
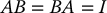
where I is the n × n identity matrix. We denote the inverse of A by A− 1. The inverse of a matrix A exists and is unique if and only if A has rank n, equivalently, if and only if the determinant  is nonzero. The matrix inverse satisfies the following
is nonzero. The matrix inverse satisfies the following
- (A− 1)− 1 = A
- (AB)− 1 = B− 1A− 1
The set of n × n nonsingular matrices over  is denoted GL(n), the general linear group of order n. Note that GL(n) is not a vector subspace of
is denoted GL(n), the general linear group of order n. Note that GL(n) is not a vector subspace of  since, for example, the sum of two invertible matrices is not necessarily invertible.
since, for example, the sum of two invertible matrices is not necessarily invertible.
B.4 Eigenvalues and Eigenvectors
The eigenvalues of a matrix A are the solutions in λ of the equation
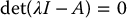
The function  is a polynomial of degree n in λ, called the characteristic polynomial of A. If λe is an eigenvalue of A, an eigenvector of A corresponding to λe is a nonzero vector xe satisfying the system of linear equations
is a polynomial of degree n in λ, called the characteristic polynomial of A. If λe is an eigenvalue of A, an eigenvector of A corresponding to λe is a nonzero vector xe satisfying the system of linear equations
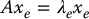
Similarity Transformation
If T is an n × n nonsingular matrix, then
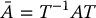
is called a similarity transformation. Since T is nonsingular, the column vectors of T are linearly independent, and hence form a basis of Rn × n. For this reason, (B.4) is also called a change of basis. The matrix  represents the same linear transformation as A in the basis defined by T.
represents the same linear transformation as A in the basis defined by T.
Diagonalizing a Symmetric Matrix
If A is a symmetric matrix, then
- its eigenvalues λ1, …, λn are real
- eigenvectors corresponding to distinct eigenvalues are orthogonal
- there exists an n × n orthogonal matrix T such that
where diag[ ] is a diagonal matrix.
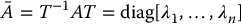
The columns of the matrix T consist of (a basis of) eigenvectors corresponding to the respective eigenvalues λ1, …, λn.
Quadratic Forms
Definition B.1.
A quadratic form on  is a scalar function
is a scalar function
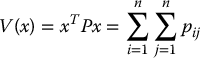
where P = (pij) is an n × n symmetric matrix. The function V, equivalently, the matrix P, is positive definite if
- xTPx > 0 for all x ≠ 0
- all eigenvalues of P are positive
- all principal minors or principal minor determinants of P are positive.
If P is positive definite, then we have the useful bounds
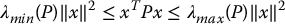
where λmin(P) and λmax(P) are, respectively, the minimum and maximum eigenvalues of P.
Range and Null Space
The range space,  , of an m × n matrix A is the subspace of
, of an m × n matrix A is the subspace of  defined by
defined by
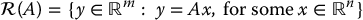
The null space,  , of an m × n matrix A is the subspace of
, of an m × n matrix A is the subspace of  defined as
defined as
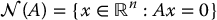
The range and null spaces of a matrix are related according to
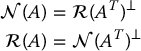
An important property of the null space is that
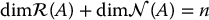
An n × n matrix is invertible if and only if the nullspace consists of only the zero vector, that is, Ax = 0 implies x = 0.
Vector Product
The vector product or cross product x × y of two vectors x and y belonging to  is a vector c defined by
is a vector c defined by
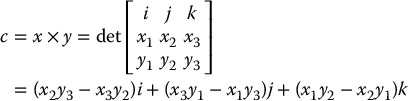
The cross product is a vector whose magnitude is
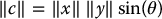
where 0 ⩽ θ ⩽ π is the angle between x and y in the plane containing them, and whose direction is given by the right hand rule shown in Figure B.1.

Figure B.1: The right hand rule.
A right-handed coordinate frame x–y–z is a coordinate frame with axes mutually perpendicular and that also satisfies the right hand rule, in the sense that k = i × j, where i, j, and k are unit vectors along the x, y, and z-axes, respectively. We can remember the right hand rule as being the direction of advancement of a right-handed screw rotated from the positive x-axis into the positive y-axis through the smallest angle between the axes. The cross product has the properties
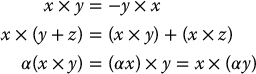
The cross product is not associative, but satisfies the Jacobi identity
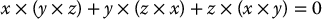
Lagrange’s formula relates the cross product and inner product according to
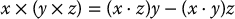
The outer product of two vectors x and y belonging to  is an n × n matrix defined by
is an n × n matrix defined by
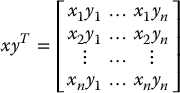
The scalar product and the outer product are related by
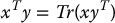
B.5 Differentiation of Vectors
Suppose that the vector x(t) = (x1(t), …, xn(t)) is a function of time. Then the time derivative  of x is the vector
of x is the vector
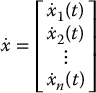
Similarly, the derivative  of a matrix A = (aij) is the matrix
of a matrix A = (aij) is the matrix  . Similar statements hold for integration of vectors and matrices. The scalar and vector products satisfy the following product rules for differentiation similar to the product rule for differentiation of ordinary functions:
. Similar statements hold for integration of vectors and matrices. The scalar and vector products satisfy the following product rules for differentiation similar to the product rule for differentiation of ordinary functions:
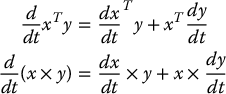
B.6 The Matrix Exponential
Given an n × n matrix M, we define the exponential, eM, of M using the series expansion
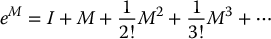
The above series expansion converges for any square matrix M and so is well defined. The matrix exponential satisfies the following properties:
- e0 = I where 0 is the n × n zero matrix and I is the n × n identity matrix
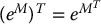
- eMeN = eM + N if MN = NM, i.e., if M and N commute
- If T is a nonsingular n × n matrix, then
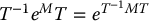
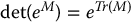
B.7 Lie Groups and Lie Algebras
Definition B.2 (Lie Group).
A Lie group is a group that is also a differentiable manifold, such that the group operations are smooth.
The most relevant examples of Lie groups for our purposes are:
- GLn(R), the general linear group over
- SO(3), the rotation group
- SE(3), the Euclidean group of rigid motions
Definition B.3 (Lie Algebra).
A Lie algebra is a vector space together with a non-associative, alternating bilinear map, (x, y)↦[x, y], called the Lie bracket, satisfying the following
- [x, x] = 0 — Alternativity
- [x1, [x2, x3]] + [x3, [x1, x2]] + [x2, [x3, x1]] — The Jacobi identity
Note that bilinearity and alternatively together imply
- [x1, x2] = −[x2, x1] — anticommutativity
Examples of Lie algebras include:
 with [x1, x2] = x1 × x2, the vector cross product
with [x1, x2] = x1 × x2, the vector cross product- quaternions, with
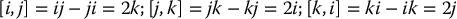
- so(3), the vector space of skew-symmetric matrices with [S1, S2] = S1S2 − S2S1, the matrix commutator. Note that it is straightforward to show that [S1, S2] is again a skew-symmetric matrix.
- vector fields on a differentiable manifold with
 , where
, where  and
and  are the Jacobians of f and g, respectively.
are the Jacobians of f and g, respectively. - se(3), the vector space of twists.
We note that a twist is defined as follows. If
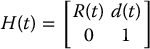
is a homogeneous transformation matrix defining a rigid motion in  , the twist associated with H is the 4 × 4 matrix
, the twist associated with H is the 4 × 4 matrix
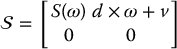
where v and ω represent the linear and angular velocities associated with the rigid motion.
The Lie Algebra of a Lie Group
Lie groups and Lie algebras are related by the exponential map. The relation between Lie groups and Lie algebras allows one to study geometric properties of Lie groups via algebraic properties of Lie algebras.
- SO(3) and so(3): every rotation matrix R in SO(3) can be expressed as eS for some skew-symmetric matrix S in so(3).
- SE(3) and se(3): every homogeneous matrix H in SE(3) can be expressed as
 , where
, where  is a twist in se(3).
is a twist in se(3).
B.8 Matrix Pseudoinverse
The inverse of a matrix A is only defined if A is a square matrix. If A is an m × n matrix, with n ≠ m, we may define a so-called pseudoinverse of A. We assume that A has full rank r = min (m, n) and we distinguish between the two cases, m < n and m > n.
If m < n, then A is a fat matrix, meaning it has more columns than rows. The right pseudoinverse of A is defined as the n × m matrix
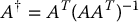
In this case AAT is m × m with full rank m and AA† = AAT(AAT)− 1 = Im × m. Given a vector  , the general solution of the equation
, the general solution of the equation
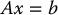
is given by x = A†b + (I − A†A)w, where  is an arbitrary vector. The vector x = A†b, i.e., with w = 0, gives the minimum norm solution ‖x‖ of Equation (B.7).
is an arbitrary vector. The vector x = A†b, i.e., with w = 0, gives the minimum norm solution ‖x‖ of Equation (B.7).
In the case m > n, then A is a tall matrix, meaning it has more rows than columns. The left pseudoinverse of A is defined as the n × m
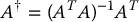
In this case ATA is n × n with full rank n and A†A = (ATA)− 1ATA = In × n. In this case A† is the least squares solution of y = Ax, i.e., the solution that minimizes the norm ‖Ax − y‖.
B.9 Schur Complement
Let M be a (p + q) × (p + q) matrix partitioned into sub-blocks as
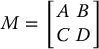
in which A, B, C, and D are, respectively, p × p, p × q, q × p, and q × q sub-matrices. Assuming that D is invertible, the Schur complement of the block D in the matrix M is the p × p matrix
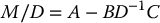
In the case that D above is singular, a generalized inverse of D can be used in place of the inverse to define a generalized Schur complement. Some properties of the Schur complement include:
- If M is a symmetric, positive definite matrix, then so is the Schur complement of D in M
- The determinant of M is
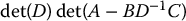
- The rank of M is equal to
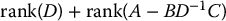
The Schur complement is useful for solving systems of equations of the form
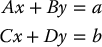
and will be useful for the study of underactuated systems in Chapter 13.
B.10 Singular Value Decomposition (SVD)
For square matrices, we can use tools such as the determinant, eigenvalues, and eigenvectors to analyze their properties. However, for nonsquare matrices these tools simply do not apply. Their generalizations are captured by the singular value decomposition (SVD).
As we described above, for  , we have
, we have  . It is easily seen that AAT is symmetric and positive semi-definite, and, therefore, has real and nonnegative eigenvalues λ1 ⩾ λ2 ⩾ ⋅⋅⋅ ⩾ λm ⩾ 0. The singular values for the matrix A are given by the square roots of the eigenvalues of AAT,
. It is easily seen that AAT is symmetric and positive semi-definite, and, therefore, has real and nonnegative eigenvalues λ1 ⩾ λ2 ⩾ ⋅⋅⋅ ⩾ λm ⩾ 0. The singular values for the matrix A are given by the square roots of the eigenvalues of AAT,
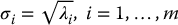
The singular value decomposition (SVD) of the matrix A is then given by
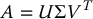
in which
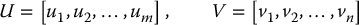
are orthogonal matrices of dimensions m × m and n × n, respectively, and Σ ∈ Rm × n is given by
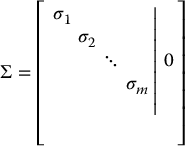
We can compute the singular value decomposition of the matrix A as follows. We begin by finding the singular values σi of A, which can then be used to find eigenvectors u1, ⋅⋅⋅, um that satisfy
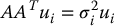
These eigenvectors comprise the columns of the matrix U = [u1, u2, …, um]. The system of equations (B.12) can be written as
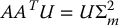
where the matrix Σm is defined as
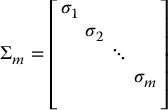
Now, define
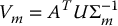
and let V be any orthogonal matrix that satisfies V = [Vm | Vn − m] (note that here Vn − m contains just enough columns so that the matrix V is an n × n matrix). It is a simple matter to combine the above equations to verify Equation (B.9).