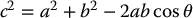Appendix A
TRIGONOMETRY

A.1 The Two-Argument Arctangent Function

The usual inverse tangent function returns an angle in the range ( − π/2, π/2). In order to express the full range of angles we will find it useful to define the so-called two-argument arctangent function,  Atan2(x, y), which is defined for all (x, y) ≠ (0, 0) and equals the unique angle θ ∈ [ − π, π] such that

(A.1)

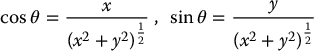
This function uses the signs of x and y to select the appropriate quadrant for the angle θ. For example, , while . If both x and y are zero, then  Atan2 is undefined.

A.2 Useful Trigonometric Formulas

Below is a list of trigonometric identities that are used to derive various expressions related to forward, inverse, and velocity kinematics.

Pythagorean Identities

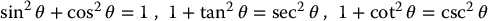
Reduction Formulas

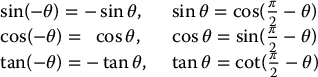
Sum-Difference Identities

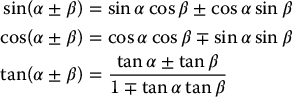
Double-Angle Identities

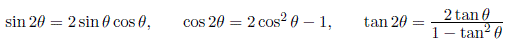
Half-Angle Identities

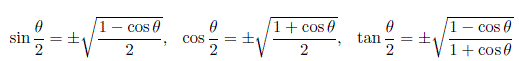
Law of Cosines

If a triangle has sides of length a, b, and c, and θ is the angle opposite the side of length c, then